Cho đường tròn (O) đường kính AB. Gọi F là điểm nằm giữa O và A. Kẻ dây CD vuôn góc với AB tại F. Trên cung nhỏ BC lấy điểm M, nối A với M cắt CD tại E. 1) Chứng minh tứ giác EFBM nội tiếp. 2) Chứng minh MA là phân giác của góc CMD và AC = AE.AM. 3) Gọi giao điểm của CB với AM là N, MD với AB là I. Chứng minh N là tâm đường tròn nội tiếp ACIM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
14 tháng 7 2017
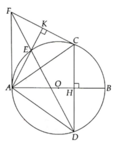
a, Học sinh tự chứng minh
b, DADB vuông tại D, có đường cao DH Þ A D 2 = AH.AB
c, E A C ^ = E D C ^ = 1 2 s đ E C ⏜ ; E A C ^ = K H C ^ (Tứ giác AKCH nội tiếp)
=> E D C ^ = K H C ^ => DF//HK (H là trung điểm DC nên K là trung điểm FC) => Đpcm

1: góc AMB=1/2*sđ cung AB=90 độ
góc EFB+góc EMB=90+90=180 độ
=>EFBM nội tiếp
2: góc AMC=1/2*sđ cung AC
góc AMD=1/2*sđcung AD
mà sđ cung AC=sđ cung AD
nên góc AMC=góc AMD
=>MA là phân giác của góc CMD
Xet ΔACE và ΔAMC có
góc ACE=góc AMC
góc CAE chung
=>ΔACE đồng dạng với ΔAMC
=>AC/AM=AE/AC
=>AC^2=AM*AE