cho hình thang ABCD (AB//CD) có 2 đường chéo cắt nhau tại O .Đường thẳng qua O và song song với đáy AB cắt AD,BC, theo thứ tự tại M,N
Chứng minh rằng \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{MN}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 3 2020
Giải toán trên mạng - Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
Bạn xem cách làm tại đây nhé!
CM
5 tháng 12 2017
Trong ΔDAB, ta có: OM // AB (gt)
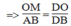(Hệ quả định lí Ta-lét) (1)
Trong ΔCAB, ta có: ON // AB (gt)
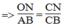(Hệ quả định lí Ta-lét) (2)
Trong ΔBCD, ta có: ON // CD (gt)
Suy ra: 
(định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra: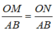 
Vậy: OM = ON
27 tháng 1 2016
Tam giác ABD có OE//AB =>DO/DB = OE/AB (Theo hệ quả Đlý Ta-lét) (1)
Tam giác ABC có OF//AB =>CO/CA = OF/AB (Theo hệ quả Đlý Ta-lét) (2)
Tam giác ABO có CD//AB =>OD/OB = OC/OA (Theo hệ quả Đlý Ta-lét)
=> OD/(OB+OD) = OC/(OA+OC) hay OD/DB=CO/CA (3)
Từ (1) (2) và (3) => OE/AB = OF/AB
=> OE = OF (điều phải chứng minh.)
Chúc bạn học giỏi nha.
AH
Akai Haruma
Giáo viên
25 tháng 2 2021
"Hai đường chéo cắt nhau tại O và song song với đáy AB....". Câu này không đúng lắm. Bạn xem lại đề.
14 tháng 3 2021
Bạn tự vẽ hình nhé
Xét \(\Delta ACD\) có OE // CD(gt)
=> \(\dfrac{OE}{DC}=\dfrac{AO}{AC}\left(1\right)\)
Xét \(\Delta BCD\) có OF // CD (gt)
=> \(\dfrac{OF}{DC}=\dfrac{BF}{FC}\left(2\right)\)
Mặt khác AB // CD nên \(\dfrac{AO}{AC}=\dfrac{BF}{FC}\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
=> \(\dfrac{OE}{DC}=\dfrac{OF}{DC}\) => OE = OF
17 tháng 2 2022
tham khảo :
https://lazi.vn/edu/exercise/582904/cho-hinh-thang-abcd-ab-cd-cheo-cat-nhau-tai-o-p
BẠN DÙNG ĐỊNH LÝ TA-LÉT ĐỂ C/M OM=ON
Vì OM // AB & OM // CD nên
\(\frac{OM}{AB}=\frac{DM}{AD}\&\frac{OM}{CD}=\frac{AM}{AD}\)
\(\Rightarrow\frac{OM}{AB}+\frac{OM}{CD}=\frac{DM}{AD}+\frac{AM}{AD}\)
\(\Leftrightarrow OM\left(\frac{1}{AB}+\frac{1}{CD}\right)=\frac{DM+AM}{AD}\)
\(\Leftrightarrow\frac{1}{AB}+\frac{1}{CD}=\frac{1}{OM}\)(1)
TƯƠNG TỰ \(\frac{1}{AB}+\frac{1}{CB}=\frac{1}{ON}\)(2)
CỘNG VẾ VỚI VẾ CỦA (1) VÀ (2) TA CÓ:
\(2\left(\frac{1}{AB}+\frac{1}{CD}\right)=\frac{1}{OM}+\frac{1}{ON}\)MÀ OM=ON(C/M TRÊN) NÊN MN=2.OM
\(\Rightarrow2\left(\frac{1}{AB}+\frac{1}{CD}\right)=\frac{1}{OM}+\frac{1}{OM}=\frac{2}{OM}\)
\(\Leftrightarrow\frac{1}{AB}+\frac{1}{CD}=\frac{2}{2.OM}=\frac{2}{MN}\left(ĐPCM\right)\)
Mình mới học lớp 5 thôi nên chỉ vẽ hình thôi à! Thông cảm nha!
Hình như sau:
Thấy đúng thì !