Giúp mình câu 22 23
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
10 tháng 3 2023
Câu 21:
\(C_nH_{2n-2}+AgNO_3+NH_3\rightarrow C_nH_{2n-3}Ag+NH_4NO_3\\ n_X=\dfrac{14-5,44}{108-1}=0,08\left(mol\right)=n_{kết.tủa}\\ M_{C_nH_{2n-3}Ag}=\dfrac{14}{0,08}=175\left(\dfrac{g}{mol}\right)=14n+107\\ \Leftrightarrow n=5\\ \Rightarrow CTPT.X:C_5H_8\\ CTCT:CH\equiv C-CH_2-CH_2-CH_3\\ CH_3-C\equiv C-CH_2-CH_3\\ CH\equiv C-CH\left(CH_3\right)-CH_3\)
Chọn C
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
10 tháng 3 2023
Câu 22:
\(n_{C_2H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\\ C_2H_2+2Br_2\rightarrow C_2H_2Br_4\\ n_{Br_2}=2.n_{C_2H_2}=2.0,1=0,2\left(mol\right)\\ m_{Br_2}=0,2.160=32\left(g\right)\\ Chọn.A\)
câu 21 22 23 24 giúp mình nha
AH
Akai Haruma
Giáo viên
1 tháng 4 2021
Câu 22:
TXĐ: $(-\infty;0]\cup [2;+\infty)$
BPT \(\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x^2-2x\leq (x+1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x\geq \frac{-1}{4}\end{matrix}\right.\Leftrightarrow x\geq \frac{-1}{4}\)
Kết hợp ĐKXĐ suy ra BPT có nghiệm $[\frac{-1}{4};0]\cup [2;+\infty)$
AH
Akai Haruma
Giáo viên
1 tháng 4 2021
Câu 23:
Theo công thức trung tuyến:
$CM^2=\frac{BC^2+AC^2}{2}-\frac{AB^2}{4}=\frac{23}{2}$
Áp dụng công thức Herong cho tam giác $ABC$:
$S_{ABC}=\sqrt{\frac{9}{2}(\frac{9}{2}-2)(\frac{9}{2}-3)(\frac{9}{2}-4)}=\frac{3\sqrt{15}}{4}$
$S_{BCM}=\frac{1}{2}S_{ABC}=\frac{3\sqrt{15}}{8}$
Áp dụng công thức: $S=\frac{abc}{4R}$ cho tam giác $BCM$ thì bán kính đường tròn ngoại tiếp tam giác là:
$R=\frac{BC.CM.BM}{4S_{BCM}}=\frac{4.\sqrt{\frac{23}{2}}.1}{\frac{3\sqrt{15}}{2}}=\frac{4\sqrt{690}}{45}$
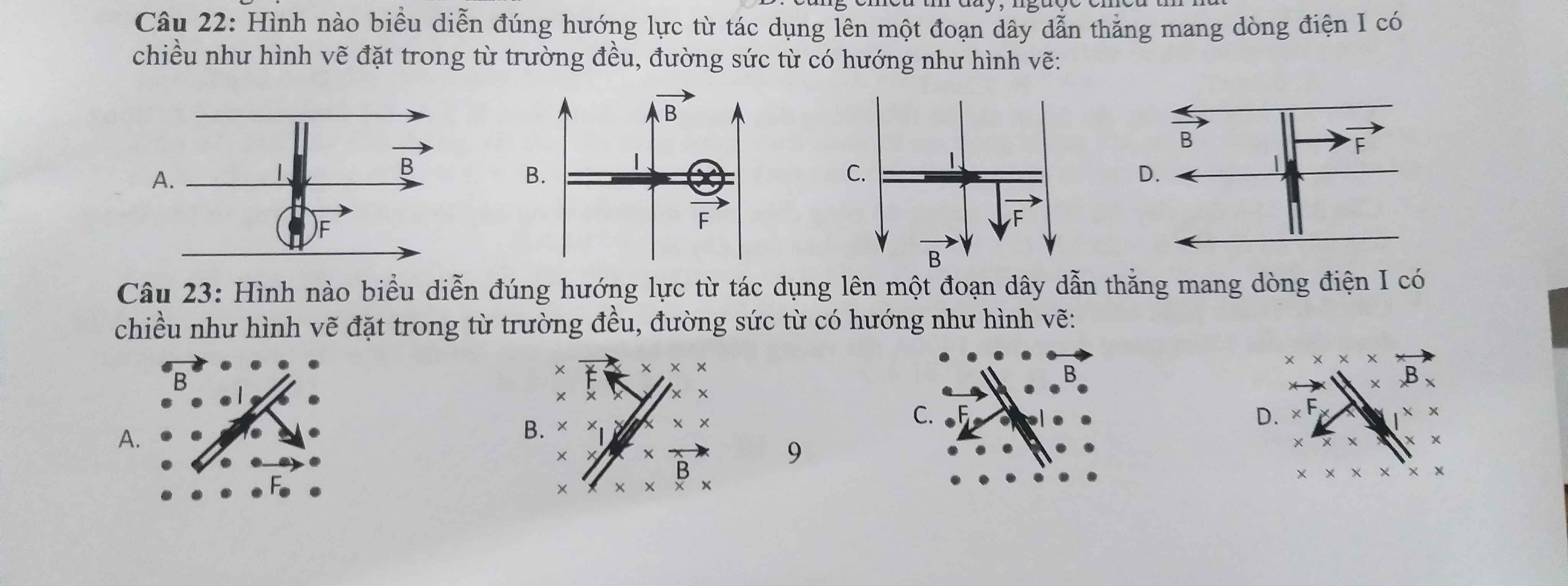
Câu 22: B
Câu 23: CTPT của Y là CnH2n+2.
→ CTPT của dẫn xuất monobrom là: CnH2n+1Br.
\(\Rightarrow M_{C_nH_{2n+1}Br}=61,5.2=123\left(g/mol\right)\)
\(\Rightarrow12n+2n+1+80=123\Rightarrow n=3\)
Vậy: Y là C3H8.
→ Đáp án: B