ho tam giác ABC kẻ AH vuông góc BC biết AB=15 cm AH= 12 HC= 16 cm .Tính độ dài các cạnh BH BC AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 7 2021
Áp dụng định lý Pi-ta-go vào tam giác vuông ABH vuông tại H ta có:
AB2= BH2 + AH2
<=> 152= 122+ AH2
<=> AH2= 152- 122= 225- 144= 81
<=> AH= 9 (cm)
Tương tự ta có : Áp dụng định lý Pi-ta-go vào tam giác vuông ACH vuông tại H .
AC2= AH2+ HC2
<=> 412= 92+ HC2
<=> HC2= 412- 92= 1681- 81= 1600
<=>HC= 40 (cm)
12 tháng 1 2018
Tam giác AHC vuông tại H nên : AC^2 = AH^2 + CH^2 = 12^2 + 16^2 = 400
=> AC = 20 (cm)
Tam giác AHB vuông tại H nên : AB^2 = AH^2 + BH^2
=> BH^2 = AB^2 - AH^2 = 13^2 - 12^2 = 25
=> BH = 5 (cm)
=> BC = BH + HC = 5 + 16 = 21 (cm)
Tk mk nha
16 tháng 2 2021
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=12^2+16^2=400\)
\(\Leftrightarrow AC=\sqrt{400}=20cm\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow BH^2=AB^2-AH^2=13^2-12^2=25\)
\(\Leftrightarrow BH=\sqrt{25}=5cm\)
Ta có: BH+CH=BC(H nằm giữa B và C)
\(\Leftrightarrow BC=5+16=21\left(cm\right)\)
Vậy: AB=20cm; BC=21cm
TT
20 tháng 4 2017
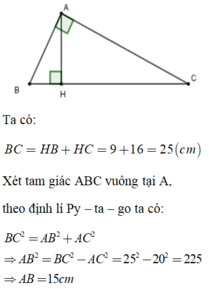
Ta có:
AC2= AH2+HC2=122+162=144+156=400.
=> AC=20(cm )
BH2=AB2-AH2=132-122
=169 - 144 = 25 => BH=5(cm)
Do đó BC=BH+HC=5+16=21(cm)
22 tháng 4 2017
Ta có:
AC2= AH2+HC2=122+162=144+156=400.
=> AC=20(cm )
BH2=AB2-AH2=132-122
=169 - 144 = 25 => BH=5(cm)
Do đó BC=BH+HC=5+16=21(cm)
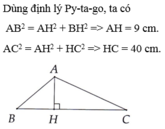
TA CÓ TAM GIÁC ABH VUÔNG TẠI H ;A/D ĐỊNH LÝ PYTAGO TA CÓ
\(AB^2=AH^2+BH^2=>BH^2=AB^2-AH^2\)
=>\(BH^2=15^2-12^2=>BH^2=81=>BH=9'\left(cm\right)\)
=>\(BC=9+16=25\left(cm\right)\)
ta có \(\Delta AHC\) VUÔNG TẠI H A/D ĐỊNHLÝ PYTAGO TA CÓ
\(AC^2=AH^2+HC^2=>AC^2=12^2+16^2\)
=>\(AC^2=400=>AC=20\left(cm\right)\)