Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn. Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) với B, C là hai tiếp điểm. Vẽ đường kính BD của đường tròn (O), AD cắt (O) tại E. Gọi H là giao điểm của OA và BC, K là trung điểm của ED.
a) Chứng minh: A, B, O, C cùng thuộc một đường tròn và OA vuông góc với BC.
b) Chứng minh: AE.AD = AC
c) Vẽ OK và cắt BC tại F. Chứng minh: FD là tiếp tuyến của đường tròn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
AB,AC là các tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
Xét tứ giác OBAC có
góc OBA+góc OCA=180 độ
nên OBAC là tứ giác nội tiếp
b: Xét ΔAEC và ΔACD có
gó ACE=góc ADC
góc EAC chung
Do đo: ΔAEC đồng dạng với ΔACD
=>AE/AC=AC/AD
=>AC^2=AE*AD

a: ΔODE cân tại O
mà OK là trung tuyến
nên OK vuông góc DE
góc OKA=góc OBA=góc OCA=90 độ
=>O,K,C,A,B cùng thuộc 1 đường tròn
b: Xét ΔACE và ΔADC có
góc ACE=góc ADC
góc CAE chung
=>ΔACE đồng dạng với ΔADC
=>AC/AD=AE/AC
=>AC^2=AD*AE
c: Xét ΔOKA vuông tại K và ΔOHF vuông tại H có
góc O chung
=>ΔOKA đồng dạng với ΔOHF
=>OK/OH=OA/OF
=>OK*OF=OH*OA=OE^2=OD^2
=>FD là tiếp tuyến của (O)

a) Xét tứ giác OBAC có
\(\widehat{OBA}\) và \(\widehat{OCA}\) là hai góc đối
\(\widehat{OBA}+\widehat{OCA}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OBAC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC


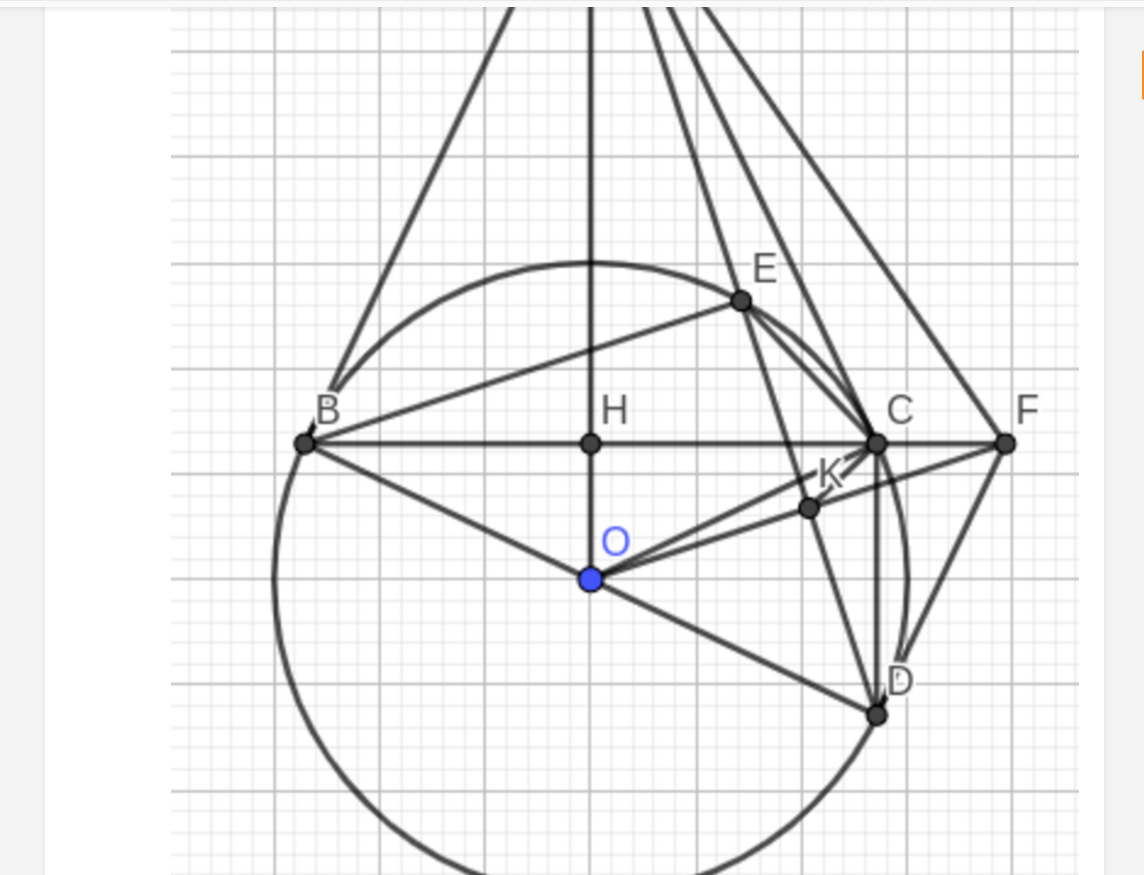
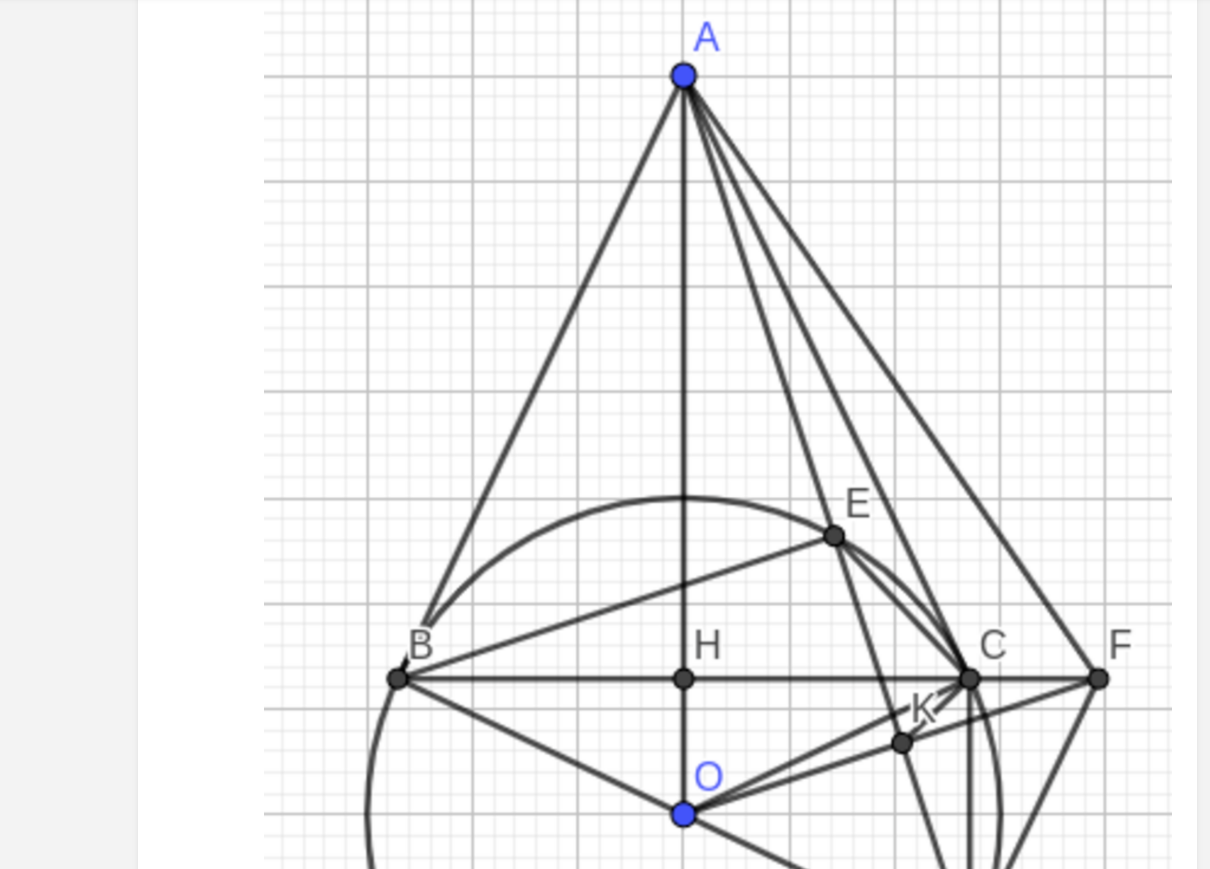
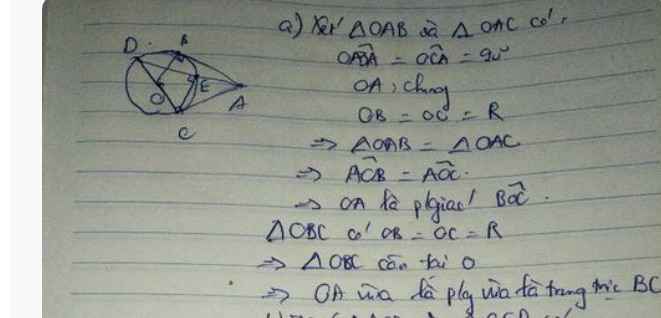

a: Xét (O) có
AB,AC là các tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
Xét tứ giác OBAC có
góc OBA+góc OCA=180 độ
nên OBAC là tứ giác nội tiếp
b: Xét ΔAEC và ΔACD có
gó ACE=góc ADC
góc EAC chung
Do đo: ΔAEC đồng dạng với ΔACD
=>AE/AC=AC/AD
=>AC^2=AE*AD