cho x,y là hai số thực thỏa mãn \(x^2+y^2-6x+5=0\). Tính giá trị lớn nhất và giá trị nhỏ nhất của P=\(x^2+y^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 8 2021
\(P=\sqrt{\left(x-3\right)^2+4^2}+\sqrt{\left(y-3\right)^2+4^2}+\sqrt{\left(z-3\right)^2+4^2}\)
\(P\ge\sqrt{\left(x-3+y-3+z-3\right)^2+\left(4+4+4\right)^2}=6\sqrt{5}\)
\(P_{min}=6\sqrt{5}\) khi \(x=y=z=1\)
Mặt khác với mọi \(x\in\left[0;3\right]\) ta có:
\(\sqrt{x^2-6x+25}\le\dfrac{15-x}{3}\)
Thật vậy, BĐT tương đương: \(9\left(x^2-6x+25\right)\le\left(15-x\right)^2\)
\(\Leftrightarrow8x\left(3-x\right)\ge0\) luôn đúng
Tương tự: ...
\(\Rightarrow P\le\dfrac{45-\left(x+y+z\right)}{3}=14\)
\(P_{max}=14\) khi \(\left(x;y;z\right)=\left(0;0;3\right)\) và hoán vị
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 9 2021
\(a^2+b^2+6ab+2=2a+3b\Rightarrow\left(a+b\right)^2-3\left(a+b\right)+2=-a\left(4b+1\right)\le0\)
\(\Rightarrow\left(a+b-1\right)\left(a+b-2\right)\le0\Rightarrow1\le a+b\le2\)
\(a^2+b^2+6ab+2=2a+3b\Rightarrow4ab=-\left(a+b\right)^2+2a+3b-2\)
\(-P=\dfrac{6a+5b+4ab+7}{a+b+1}=\dfrac{6a+5a+7-\left(a+b\right)^2+2a+3b-2}{a+b+1}\)
\(=\dfrac{-\left(a+b\right)^2+8\left(a+b\right)+5}{a+b+1}\)
Tới đây có thể giải theo lớp 9 (tách thành tích hoặc bình phương) hoặc làm theo lớp 12 (khảo sát hàm \(f\left(x\right)=\dfrac{-x^2+8x+5}{x+1}\) trên \(\left[1;2\right]\)). Cả 2 việc đều dễ dàng cả
\(-P=6-\dfrac{\left(x-1\right)^2}{x+1}=\dfrac{17}{3}+\dfrac{\left(3x-1\right)\left(2-x\right)}{3\left(x+1\right)}\)
CM
17 tháng 4 2017
Đáp án C
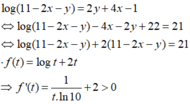
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
CM
23 tháng 7 2019
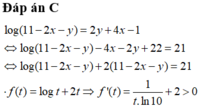
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
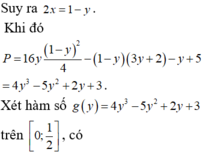
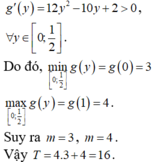
\(x^2+y^2=6x-5\)
\(\left(x-3\right)^2+y^2=2^2\Rightarrow1\le x\le5\)
\(1\le x^2+y^2\le25\)