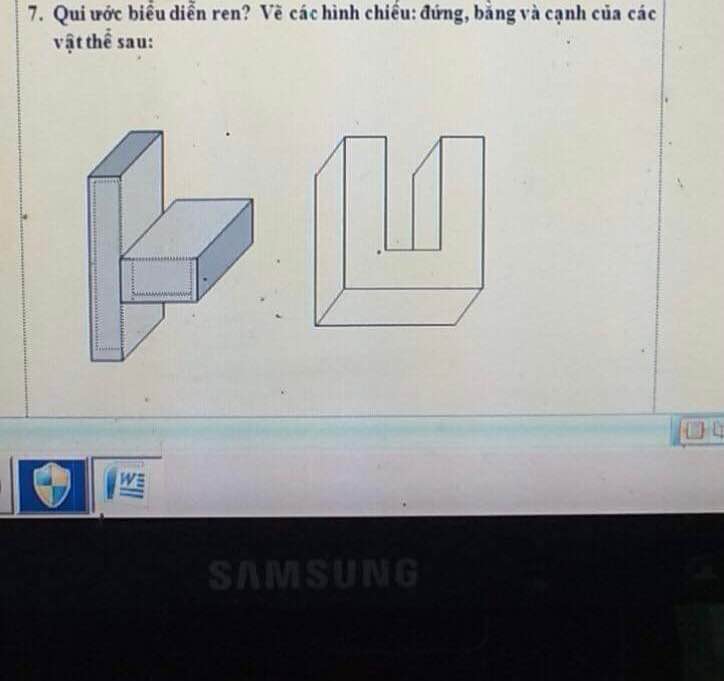
Giúp mình bài này với, mai mình thi rồi hic
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ :\(\left\{{}\begin{matrix}x+1\ge0\\x^2+1\ge0\end{matrix}\right.\Leftrightarrow x\ge-1\)
Khi đó \((x^2+4x+5)\sqrt{x+1}=(3x^2-8x-5)\sqrt{x^2+1}\)
\(\Leftrightarrow(x^2+1)\sqrt{x+1}+4(x+1)\sqrt{x+1}=3(x^2+1)\sqrt{x^2+1}-8(x+1)\sqrt{x^2+1}\)
Đặt \(\sqrt{x+1}=a;\sqrt{x^2+1}=b(a\ge0;b>0)\)
Phương trình trở thành :
\(4a^3+ab^2=3b^3-8a^2b\)
\(\Leftrightarrow4(a^3+b^3)+b(8a^2+ab-7b^2)=0\)
\(\Leftrightarrow(a+b)(4a^2-4ab+4b^2)+(a+b)(8ab-7b^2)=0\)
\(\Leftrightarrow(a+b)(4a^2+4ab-3b^2)=0\)
\(\Leftrightarrow\left(a+b\right)\left(2a-b\right)\left(2a+3b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=0(\text{loại})\\2a-b=0\\2a+3b=0(\text{loại})\end{matrix}\right.\Leftrightarrow2a=b\) (vì \(\left\{{}\begin{matrix}a\ge0\\b>0\end{matrix}\right.\) nên a+b>0 ; 2a +3b > 0)
Trở lại cách đặt ta được
\(2\sqrt{x+1}=\sqrt{x^2+1}\Leftrightarrow x^2-4x-3=0\)
\(\Leftrightarrow x=\pm\sqrt{7}+2\) (loại \(x=-\sqrt{7}+2\))
Vậy x = \(\sqrt{7}+2\) là nghiệm phương trình

a) Điện trở tương đương của đoạn mạch :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)
b) Hiệu điện thế giữa hai đầu đoạn mạch :
\(U=I.R_{tđ}=2.24=48\left(V\right)\)
⇒ \(U=U_1=U_2=48\left(V\right)\) (vì R1 // R2)
Cường độ dòng điện chạy qua mỗi điện trở :
\(I_1=\dfrac{U_1}{R_1}=\dfrac{48}{60}=0,8\left(A\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{48}{40}=1,2\left(A\right)\)
Chúc bạn học tốt

– Thân to ra do sự phân chia các tế bào của mô phân sinh: tầng sinh vỏ, tầng sinh trụ. ... Hằng năm sinh ra phía ngoài một lớp tế bào vỏ, phía trong một lớp thịt vỏ. + Tầng sinh trụ nằm giữa mạch rây và mạch gỗ, hằng năm sinh ra phía ngoài một lớp mạch rây, phía trong một lớp mạch gỗ, bóc theo vỏ.
#CHUCBANTHITOT


\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)


1:
a: =>(x-1)(x-7)=0
=>x=1 hoặc x=7
b: =>x(x^2-9x+8)=0
=>x(x-1)(x-8)=0
=>\(x\in\left\{0;1;8\right\}\)
c: Đặt 1/căn x-7=a; 1/căn y+6=b
Theo đề, ta có:
7a-4b=5/3 và 5a+3b=13/6
=>a=1/3 và b=1/6
=>x-7=9 và y+6=36
=>x=16 và y=30
Bài 3:
a: Δ=(2m+3)^2-4(m^2+3m+2)
=4m^2+12m+9-4m^2-12m-8=1>0
=>PT luôn có hai nghiệm pb
b: x1^2+x2^2=1
=>(x1+x2)^2-2x1x2=1
=>(2m+3)^2-2(m^2+3m+2)=1
=>4m^2+12m+9-2m^2-6m-4-1=0
=>2m^2+6m+4=0
=>m=-1 hoặc m=-2
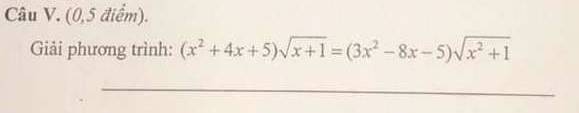
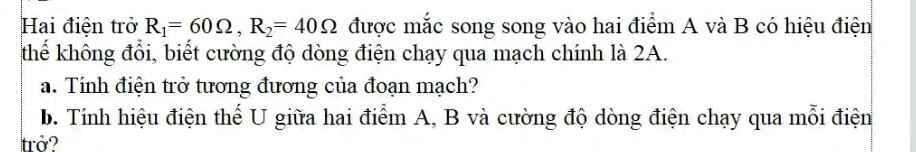
 giúp mình câu 17 với hic mai thi r 😿👉👈
giúp mình câu 17 với hic mai thi r 😿👉👈