Giải bài toán sau = cách lập phươnh trình:
Tính độ dài 2 cạnh góc vuông của 1 tam giác vuông nội tiếp đường tròn bán kính 6,5 cm. Biết rằng 2 cạnh góc vuông cuar tam giác hơn kém nhau 7 cm.
Help me. Giúp e vs ạ. Please...
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ dài 1 cạnh góc vuông là x (cm, x>7)
độ dài 1 cạnh góc vuông còn lạ là x-7 (cm)
Theo đè là ta có
\(x^2+\left(x-7\right)^2=13^2\)(ĐL Pytago)
\(\Leftrightarrow x^2+x^2-14x+49=169\)
\(\Leftrightarrow2x^2-14x-120=0\)
\(\Leftrightarrow x^2-7x-60=0\)
\(\Leftrightarrow x^2-12x+5x-60=0\)
\(\Leftrightarrow x.\left(x-12\right)+5.\left(x-12\right)=0\)
\(\Leftrightarrow\left(x-12\right).\left(x+5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-12=0\\x+5=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=12\left(TM\right)\\x=-5\left(L\right)\end{cases}}\)
Vậy độ dài 1 cạnh góc vuông là 12cm
dộ dài 1 cạnh góc vuông còn lại là \(12-7=5\left(cm\right)\)
Nhớ k cho mình nhé

Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
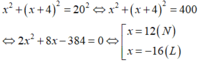
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm

Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
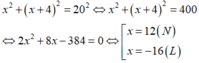
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm

Lời giải:
Gọi cạnh góc vuông lớn là $a+5$, cạnh góc vuông nhỏ là $a$ (cm)
Áp dụng định lý Pitago:
$a^2+(a+5)^2=25^2$
$\Leftrightarrow 2a^2+10a-600=0$
$\Leftrightarrow a^2+5a-300=0$
$\Leftrightarrow (a-15)(a+20)=0$
$\Rightarrow a=15$ (do $a>0$)
Vậy cạnh góc vuông thứ nhất là $15$, cạnh góc vuông thứ hai là $20$