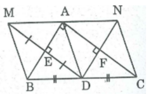
Cho tam giác ABC vuông tại A và D là trung điểm của BC. Gọi M là điểm đối xứng của D qua AB . E là giao điểm của DM và AB. gọi N là điểm đối xưng của D qua AC, F là giao điểm của DN và AC .
a, Tứ giác AEDF là hình gì ? vì sao ?
b, Tứ giác ADBM là hình gì ? Vì sao ?
c, Chứng minh M đối xứng với N qua A
d, Tam giác vuông ABC cần có thêm điều kiện gì thì tứ giác AEDF là hình vuông ?
giúp mk vs mk cần gấp

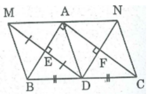
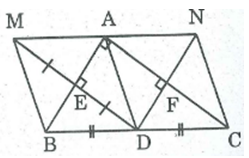
Em tham khảo tại đây nhé.
Câu hỏi của nguuen thi minh tam - Toán lớp 8 - Học toán với OnlineMath