cho parapol (P): y=x2 và đường thẳng (d): y=-x+2
a) vẽ đồ thị (P) và (d) trên cùng một hệ trục tọa độ
b) tìm tọa độ giao điểm của (d) và (P) bằng phép toán
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 5 2021
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=-x+2\)
\(\Leftrightarrow x^2+x-2=0\)(1)
a=1; b=1; c=-2
Vì a+b+c=0 nên phương trình (1) có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{-2}{1}=-2\)
Thay x=1 vào (d), ta được:
y=-1+2=1
Thay x=-2 vào (d), ta được:
y=-(-2)+2=2+2=4
Vậy: (P) và (d) có hai tọa độ giao điểm là (1;1) và (-2;4)
26 tháng 3 2023
a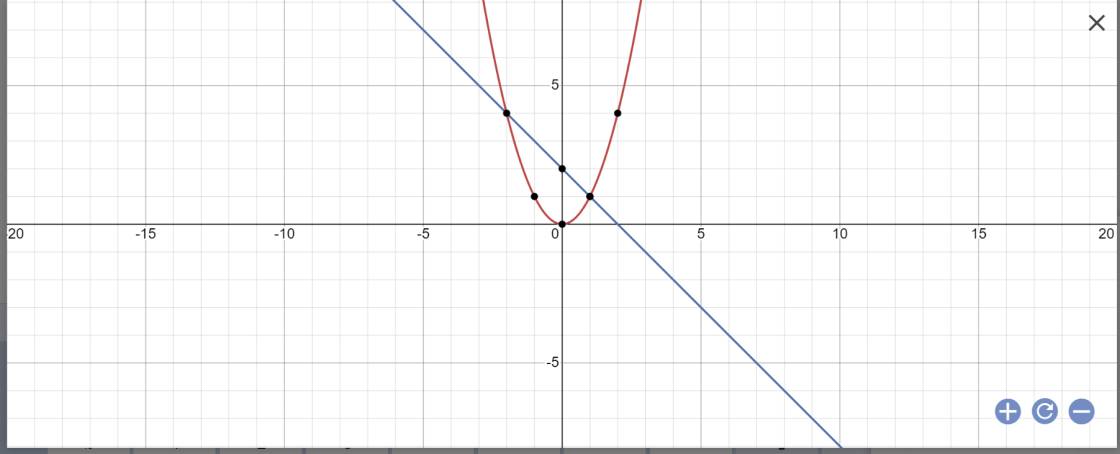
b:
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1
1 tháng 7 2023
1:
a: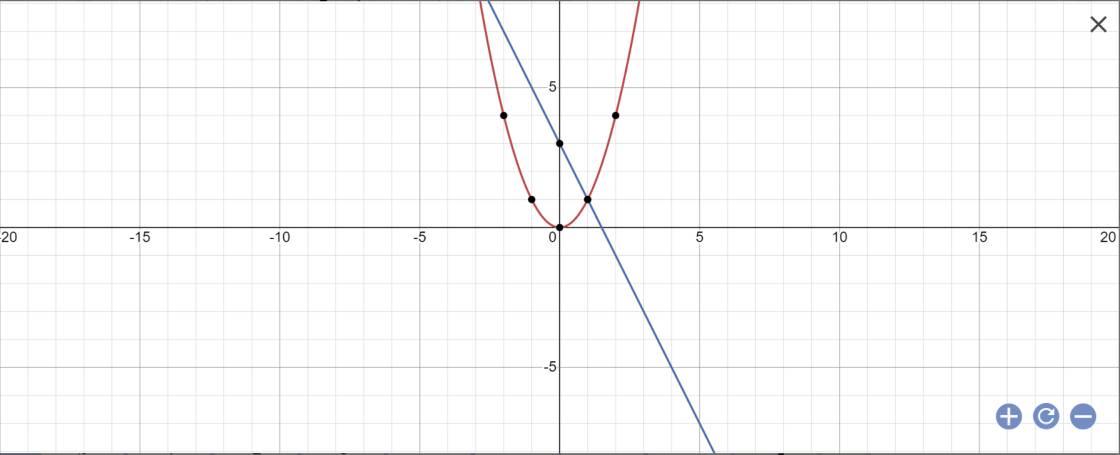 
b: PTHĐGĐ là:
x^2+2x-3=0
=>(x+3)(x-1)=0
=>x=-3 hoặc x=1
=>y=9 hoặc y=1
MN
13 tháng 3 2019
a,
| -4 | -2 | 0 | 2 | 4 | |
| \(y=\frac{1}{4}x^2\) | 4 | 1 | 0 | 1 | 4 |
| \(y=-\frac{1}{2}x+2\) | 4 | 3 | 2 | 1 | 0 |
Bạn tự vẽ ha.
b,
Phương trình hoàng độ giao điểm của (p) và (d) là:
\(\frac{1}{4}x^2=-\frac{1}{2}x+2\)
\(\Leftrightarrow\frac{1}{4}x^2+\frac{1}{2}x-2=0\Leftrightarrow x^2+2x-8=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x=-4\\x=2\end{cases}}\)
\(x=-4\Rightarrow y=4\)
\(x=2\Rightarrow y=1\)
Vậy tọa độ giao điểm của (p) và (d) là (-4;4) ; (2;1)
29 tháng 2 2020
Bạn tham khảo link này nha:
https://olm.vn/hoi-dap/detail/214561933532.html
Chúc bạn học tốt
Forever
7 tháng 11 2021
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x=x-1\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
26 tháng 2 2023
a)
\(\left(P\right):y=x^2\)
Ta có bảng
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 4 |
Vậy đồ thị hàm số \(y=x^2\) là một parabol lần lượt đi qua các điểm
\(\left(-2;4\right),\left(-1;1\right),\left(0;0\right),\left(1;1\right),\left(2;4\right)\)
Bạn tự vẽ nhé
\(\left(d\right):y=-2x+3\)
Cho \(y=0\Rightarrow x=\dfrac{3}{2}\Rightarrow A\left(\dfrac{3}{2};0\right)\in Ox\)
Cho \(x=0\Rightarrow y=3\Rightarrow B\left(0;3\right)\in Oy\)
Vẽ đường thẳng AB ta được đths \(y=-2x+3\)
Bạn tự bổ sung vào hình vẽ nhé
b) Xét PTHĐGĐ của \(\left(P\right),\left(d\right)\) là nghiệm của phương trình
\(x^2=-2x+3\\ \Leftrightarrow x^2+2x-3=0\)
Xét \(a+b+c=1+2-3=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Với `x=1 => y=x^2 = 1`
Với `x=2 => y=x^2 = 4`
Vậy tọa độ giao điểm của \(\left(P\right),\left(d\right)\) là 2 điểm \(\left(1;1\right)\) và \(\left(2;4\right)\)
a) Bạn tự vẽ
b) Phương trình hoành độ giao điểm của (P) và (d)
\(x^2=-x+2\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
+) Với \(x=1\) thì \(y=1\)
+) Với \(x=-2\) thì \(y=4\)
Vậy (P) cắt (d) tại 2 điểm \(\left(1;1\right)\) và \(\left(-2;4\right)\)