Một bồn nước inox có dạng một hình trụ với chiều 1,75m và diện tích đáy là 0,32 m2. Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề dày của bồn nước).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 2 2017
Đáp án B
Yêu cầu bài toán “Tìm R để diện tích toàn phần của hình truh là nhỏ nhất”
Gọi h là chiều cao của hình trụ Thể tích khối trụ là V = π R 2 h = 10 ⇒ h = 10 π R 2 1
Diện tích toàn phần của hình trụ là: S T P = S x q + 2 × S d = 2 π R h + 2 π R 2 2
Từ (1); (2) suy ra S T P = 2 π R 2 + 20 R = 2 π R 2 + 10 R + 10 R ≥ 3 200 π 3
Dấu = xảy ra khi và chỉ khi 2 π R 2 = 10 R ⇔ R = 5 π 3 m
CM
3 tháng 7 2019
Đáp án B.
Gọi h(m) là chiều cao của chiếc bồn nước, h > 0 .
Thể tích của chiếc bồn là V = π r 2 h = 10 ⇒ h = 10 π r 2 .
Diện tích toàn phần của chiếc bồn là:
S t p = 2 π r 2 + 2 π r h = 2 π r 2 + 2 π r . 10 π r 2 = 2 π r 2 + 20 r = 2 π r 2 + 10 r + 10 r
Cách 1: Theo bất đẳng thức Côsi ta có: S t p ≥ 3 2 π r 2 . 10 r . 10 r 3 = 3. 200 π 3 .
Dấu “=” xảy ra khi
2 π r 2 = 10 r ⇔ r 3 = 5 π ⇔ r = 5 π 3
Vậy với r = 5 π 3 thì lượng inox được sử dụng để làm bồn nước là ít nhất.
Cách 2: Xét hàm số f r = 2 π r 2 + 20 r , r > 0 .
Ta có
f ' r = 4 π r − 20 r 2 = 4 π r 3 − 20 r 2 ; f ' r = 0 ⇔ 4 π r 3 − 20 = 0 ⇔ r 3 = 5 π ⇔ r = 5 π 3
Bảng biến thiên:
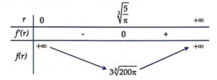
⇒ f r đạt giá trị nhỏ nhất tại r = 5 π 3 .
SM
29 tháng 3 2020
Bài giải
Ta áp dụng công thức:
V = S . h = 0,32 . 1,75 = 0,53 (m \(^3\))
Vậy bồn nước này đựng đầy 3 mét khối nước
17 tháng 6 2020
Thể tích của chiếc bồn là:
1,8 x ( 0,6 x 0,6 x 3,14 ) = 2,03472 ( m^3)
Bồn đó chứa được số lí dầu là:
2,03472 x 1000 = 2034,72 ( lít )
Đáp số....
CM
31 tháng 8 2017
Diện tích bể mặt bốn không có nắp bằng diện tích xung quanh cộng thêm diện tích mặt đáy.
Diện tich xung quanh bằng: S x q =(5,3 + 112,5).2.2,1 =74,76 ( m 2 )
Diện tích đáy: S đ á y = 5,3 . 12,5= 66,25 ( m 2 )
Diện tích bề mặt bồn bằng: 74,76 + 66,25 = 141,01 ( m 2 )
