Cho hình vuông ABCD có cạnh bằng a. Gọi E là một điểm bất kỳ trên cạnh BC. Qua B vẽ đường thẳng vuông góc với tia DE tại H, đường thẳng này cắt tia DC tại F.
a) Chứng minh rằng: Năm điểm A, B, H, C, D cùng nằm trên một đường tròn.
b) Chứng minh rằng: DE.HE = BE.CE.
c) Tính độ dài đoạn thẳng DH theo a khi E là trung điểm của BC.
d) Chứng minh rằng: HC là tia phân giác của ![]() .
.

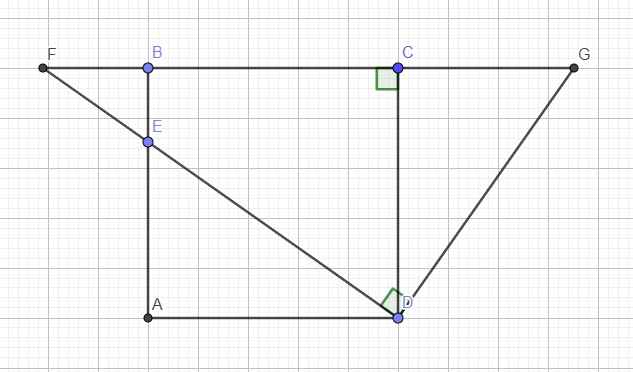

a: góc BAD=góc BCD=góc BHD=90 độ
=>A,B,H,C,D cùng nằm trên 1 đường tròn
b: Xét ΔEHB vuông tại H và ΔECD vuông tại C có
góc HEB=góc CED
=>ΔEHB đồng dạng với ΔECD
=>EH/EC=EB/ED
=>EH*ED=EB*EC