BÀI 1 : Gọi AM, BN, CL là ba đường cao của tam giác ABC .Chứng minh
a) tam giác ANL đồng dạng tam giác ABC
b) AN.BL.CM=AB.BC.CA.cosA.cosB.cosC
BÀI 2: Cho tam giác ABC vuông tại A , AB=6cm, AC=8cm
a) Tính BC, góc B, góc C
b) phân giác của góc A cắt BC tại D .Tính BD,CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 3 2023
a: Xet ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
AH=6*8/10=4,8cm
BH=6^2/10=3,6cm
CM
12 tháng 10 2018
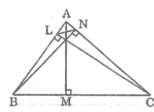
a. Xét hai tam giác BNA và CLA, ta có:
∠ BNA = ∠ CLA = 90 °
góc A chung
Suy ra ∆ BNA đồng dạng ∆ CLA (g.g)
Suy ra: AL/AN = AC/AB ⇒ AL/AC = AN/AB
Xét hai tam giác ABC và ANL, ta có:
AL/AC = AN/AB
góc A chung
Suy ra ∆ ABC đồng dạng ∆ ANL (c.g.c)
1 tháng 5 2021
a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
1 tháng 5 2021
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
9 tháng 3 2022
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
Do đó: ΔHBA\(\sim\)ΔABC
b: BC=10cm
AH=4,8cm
BH=3,6cm
c: DB/DC=AB/AC=6/8=3/4
