Cho tam giác ABC vuông tại A có AC = 12cm, BC = 13cm. Vẽ tia phân giác BM cửa góc ABC ( M thuộc AC). Từ M kẻ MD vuông góc với BC tại D
a) So sánh các góc của tam giác ABC b) Chứng minh tam giác ABM = tam giác DBM c) Đường thẳng DM cắt tia BA tại K, Chứng minh KD + AB > BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 4 2020
Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
LA
8 tháng 4 2020
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A
DT
20 tháng 3 2019
a, xét tam giác AMB và tam giác AMC có:
AB=AC(gt)
\(\widehat{BAM}\) =\(\widehat{CAM}\)(gt)
AM chung
suy ra tam giác AMB= tam giác AMC(c.g.c)
b,xét tam giác AHM và tam giác AKM có:
AM cạnh chung
\(\widehat{HAM}\)=\(\widehat{KAM}\)(gt)
suy ra tam giác AHM=tam giác AKM(CH-GN)
Suy ra AH=AK
c,gọi I là giao điểm của AM và HK
xét tam giác AIH và tam giác AIK có:
AH=AK(theo câu b)
\(\widehat{IAH}\)=\(\widehat{IAK}\)(gt)
AI chung
suy ra tam giác AIH=tam giác AIK (c.g.c)
Suy ra \(\widehat{AIH}\)=\(\widehat{AIK}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{AIH}\)=\(\widehat{AIK}\)= 90 độ
\(\Rightarrow\)HK vuông góc vs AM
KV
11 tháng 3 2023
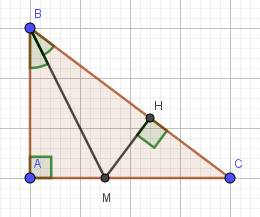
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)
6 tháng 4 2022
a: BC=15cm
Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
Suy ra: AD=HD
