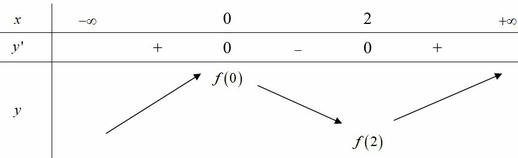
1, Cho hàm số y=f(x) và f'(0)=3. Hỏi giới hạn \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-1}{f\left(0\right)-f\left(x\right)}\)=?
2, Cho hàm số f(x) có đạo hàm trên R và f'(x)=0 có các nghiệm là 1 và -2. Đặt \(g\left(x\right)=f\left(\sqrt{x^2+4}\right)\), hỏi g'(x)=0 có bao nhiêu nghiệm?
Mọi người giúp mình với ạ, mình cần gấp!! Cảm ơn mọi người rất nhiều!!!




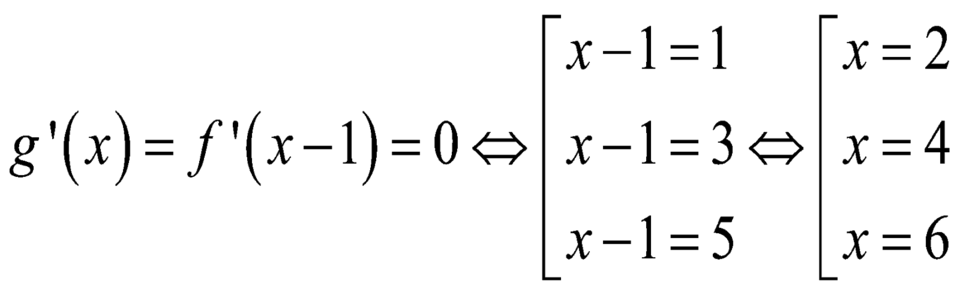






1. Áp dụng quy tắc L'Hopital
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-1}{f\left(0\right)-f\left(x\right)}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{1}{2\sqrt{x+1}}}{-f'\left(0\right)}=-\dfrac{1}{6}\)
2.
\(g'\left(x\right)=2x.f'\left(\sqrt{x^2+4}\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(\sqrt{x^2+4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\sqrt{x^2+4}=1\\\sqrt{x^2+4}=-2\end{matrix}\right.\)
2 pt cuối đều vô nghiệm nên \(g'\left(x\right)=0\) có đúng 1 nghiệm