Cho hàm số y = f(x) = x2 + 4x + 3 có đồ thị như hình vẽ:Tìm m để: |f(x) - 2| = m + 1 có 3 nghiệm phân...
Đọc tiếp
Cho hàm số y = f(x) = x2 + 4x + 3 có đồ thị như hình vẽ:
Tìm m để: |f(x) - 2| = m + 1 có 3 nghiệm phân biệt
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
9 tháng 5 2022
x2+4x+2m+1=0 \(\Leftrightarrow\) x2+4x+3=-2m+2.
Phương trình đã cho có tối đa một nghiệm âm, xảy ra khi -2m+2>3.
Vậy không có giá trị nào của m thỏa yêu cầu đề bài.
HN
9 tháng 5 2022
Xin lỗi! Mình bất cẩn, bạn kiểm tra lại đồ thị giúp mình, bạn nhầm đồ thị rồi!
Giải:
x2+4x+2m+1=0 ⇔ x2+4x+3=-2m+2.
f(0)=3.
Ycđb \(\Leftrightarrow\) -1<-2m+2<3 \(\Rightarrow\) -1/2<m<3/2.
HN
9 tháng 5 2022
Bạn kiểm tra đồ thị giúp mình, nhầm đồ thị rồi!
x2+4x+m-3=0 \(\Leftrightarrow\) x2+4x+3=6-m.
f(-3)=0.
Ycđb \(\Leftrightarrow\) 6-m>0 \(\Rightarrow\) m<6.
CM
5 tháng 9 2018
Chọn B
Đặt t = x 2 - 2 x với x ∈ - 3 2 ; 7 2
Bảng biến thiên của hàm số t = x 2 - 2 x trên đoạn - 3 2 ; 7 2 là:
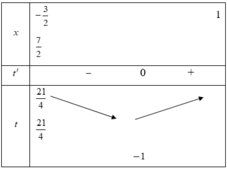
Dựa vào bảng biến thiên t ∈ - 1 ; 21 4
Khi đó phương trình f ( x 2 - 2 x ) = m (1) trở thành f(t)=m (2).
Ta thấy, với mỗi giá trị t ∈ ( - 1 ; 21 4 ] ta tìm được hai giá trị của x ∈ - 3 2 ; 7 2
Do đó, phương trình (1) có 4 nghiệm thực phân biệt thuộc - 3 2 ; 7 2 khi và chỉ khi phương trình (2) có hai nghiệm thực phân biệt thuộc ( - 1 ; 21 3 ]
Đường thẳng y=m cắt đồ thị hàm số y=f(t) tại hai điểm phân biệt có hoành độ thuộc - 1 ; 21 4
Dựa vào đồ thị ta thấy chỉ có hai giá trị nguyên của m thỏa yêu cầu là m=3 và m=5
