cho nữa đường tròn tâm O bán R đường kính AB=2R ax by là các tia vuông góc AB. qua M thay đổi trên nửa đường tròn kẻ tiếp tuyến vuông góc với nữa đường tròn lần lượt cắt Ax, By tai C và D
a) chứng minh:A , C, M, O thuộc một đường tròn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vao nhe http://files.hoconline-vn.webnode.vn/200000034-0b01c0bfd5/MOT%20SO%20BAI%20TAP%20ON%20THI%20VAO%20LOP%2010.swf
Vào thử đi : http://files.hoconline-vn.webnode.vn/200000034-0b01c0bfd5/MOT%20SO%20BAI%20TAP%20ON%20THI%20VAO%20LOP%2010.swf
**** cho mình nhé

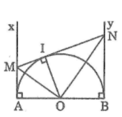
Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có:
O I 2 = MI.NI
Mà: MI = MA, NI = NB (chứng minh trên)
Suy ra : AM.BN = O I 2 = R 2

1: Xét tứ giác OACM có
góc OAC+góc OMC=180 độ
=>OACM là tứ giác nội tiếp
2: Xét (O) có
CA,CM là tiếp tuyến
nên OC là đường phân giác của góc AOM(1)
Xét (O) có
DM,DB là tiếp tuyến
nen DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
=>OC vuông góc OD
=>1/OM^2=1/OC^2+1/OD^2=1/R^2
Ta có: \(\widehat{OAC}=90^0\) (giả thiết); \(\widehat{OMC}=90^0\) (tính chất tiếp tuyến)
Tứ giác \(ACMO\) có: \(\widehat{OAC}+\widehat{OMC}=90^0+90^0=180^0\)
\(\Rightarrow ACMO\) nội tiếp