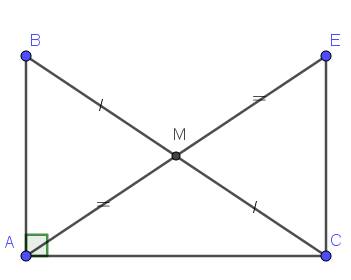
Cho tam giác ABC vuông tại B. Vẽ trung tuyến AM. Trên tia đối của MA lấy điểm E sao cho ME= MA. CHứng minh rằng a) tam giác AMB= EMC b) AC>CE c) góc BAM > góc MAC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
26 tháng 12 2022
Lời giải:
a.
Xét tam giác $AMB$ và $EMC$ có:
$\widehat{AMB}=\widehat{EMC}$ (đối đỉnh)
$AM=EM$
$MB=MC$
$\Rightarrow \triangle AMB=\triangle EMC$ (c.g.c)
b.
Vì $\triangle AMB=\triangle EMC$ nên $\widehat{MAB}=\widehat{MEC}$
Mà 2 góc này ở vị trí so le trong nên $EC\parallel AB$
Mà $AB\perp AC$ nên $EC\perp AC$ (đpcm)
c.
Vì $\triangle AMB=\triangle EMC$ nên:
$AB=EC$
Vì $EC\perp AC$ nên $\widehat{ECA}=90^0=\widehat{BAC}$
Xét tam giác $ECA$ và $BAC$ có:
$\widehat{ECA}=\widehat{BAC}=90^0$ (cmt)
$AC$ chung
$EC=BA$ (cmt)
$\Rightarrow \triangle ECA=\triangle BAC$ (c.g.c)
$\Rightarrow EA=BC$
Mà $EA=2AM$ nên $2AM=BC$ (đpcm)
15 tháng 4 2022
a: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)
MB=MC
Do đó: ΔMAB=ΔMEC
b: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AB//EC
4 tháng 5 2016
Bạn tự vẽ hình nha, mk ko biết cách up hình lên
Giải:
a) Xét hai tam giác ABM và tam giác ECM có:
MB = MC (gt)
MA = ME (gt)
góc AMB = góc EMC (đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta EMC\left(c.g.c\right)\)
b) Xét 2 tg ACM và tg EBM có:
MA = ME (gt)
MC = MB (gt)
góc AMC = góc EMB (đối đỉnh)
\(\Rightarrow\Delta ACM=\Delta EBM\left(c.g.c\right)\)
\(\Rightarrow AC=EB\) (2 cạnh tương ứng)
Trong tg BCE có: góc BCE = \(90^0\) (góc tương ứng với góc ABM)
\(\Rightarrow\) BE là cạnh huyền
\(\Rightarrow\) BE > CF hay AC > CF
C
15 tháng 3 2017
a.
MB = MC (AM là trung tuyến)
\(\widehat{AMB}\) = \(\widehat{EMC}\) (Góc đối)
MA = ME (Giả thuyết)
=> Tam giác ABM = Tam giác ECM (Cạnh - góc - cạnh)
b.
Tam giác ABM = Tam giác ECM
ABM là tam giác vuông tại B
=> Tam giác ECM vuông tại C
=> EC vuông góc BC
Mà AB vuông góc BC
=> EC song song AB
c.
Ta có
\(\widehat{BAM}\) = 180o - 90o - \(\widehat{AMB}\)(1)
\(\widehat{MAC}\) = 180o - \(\widehat{ACM}\) - \(\widehat{AMC}\)
=> \(\widehat{MAC}\) = 180 - \(\widehat{ACM}\) - (180o - \(\widehat{AMB}\))
=> \(\widehat{MAC}\) = \(\widehat{ACM}\) - \(\widehat{AMB}\)(2)
(1) và (2) => \(\widehat{BAM}\) > \(\widehat{MAC}\)(Vì góc \(\widehat{ACM}\) < 90o)
a: Xét ΔMAB và ΔMEC có
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔMAB=ΔMEC
b: AC>AB
=>AC>CE
c: góc BAM=góc CEA
mà góc CEA>góc CAM
nên góc BAM>góc CAM