Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)BH vuông góc với AC
CD vuông góc với AC =>BH//CD
Tương tự HC//BD =>BDCH là HBH
b)góc BDC=góc BHC
HC cắt AB tại E => góc AEH=900
HB cắt AC tại F => góc AFH=900
=>góc EHF=góc BHC= góc BDC
góc AEH+góc AFH+góc EHF+góc ABC =3600
=>góc BDC+góc ABC=1800
a)BH vuông góc với AC
CD vuông góc với AC =>BH//CD
Tương tự HC//BD =>BDCH là HBH
b)góc BDC=góc BHC
HC cắt AB tại E => góc AEH=900
HB cắt AC tại F => góc AFH=900
=>góc EHF=góc BHC= góc BDC
góc AEH+góc AFH+góc EHF+góc ABC =3600
=>góc BDC+góc ABC=1800
a: Xét tứ giác BDCH có
BH//CD
BD//CH
Do đó: BDCH là hình bình hành
b: \(\widehat{BDC}=180^0-60^0=120^0\)
a: Xét tứ giác BDCH có
BD//CH
BH//CD
Do đó: BDCH là hình bình hành
b: Xét tứ giác ABDC có \(\widehat{ABD}+\widehat{ACD}=180^0\)
nên ABDC là tứ giác nội tiếp
Suy ra: \(\widehat{BDC}=180^0-\widehat{BAC}=120^0\)
a) Vì BHCD có các cặp cạnh đối song song nên là hình bình hành.
b) Tứ giác ABCD có A B D ^ = A C D ^ = 90 0 m à B A C ^ = 60 0 nên B D C ^ = 120 0
a: Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
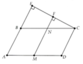
a/ Do H là trực tâm => BH vuông góc với AC mà DC vuông góc với AC => BH//CD
Tương tự cũng có CH//BD
=> BDCH là hình bình hành (Tứ giác có các cặp cạnh dối // với nhau từng đôi một là hbh)
b/ Xét tứ giác ABDC có tổng các góc trong =360
=> ^BAC+^BDC+^ABD+ACD=^BAC+^BDC+90+90=360 => ^BAC+^BDC=180
c/ Nối H với D cắt BC tại M', do BDCH là hình bình hành => M'B=M'C (t/c đường chéo hbh) => M trùng M' => H; M; D thẳng hàng
d/ Xét tam giác ADH có
OA=OD
MH=MD (t/c đường chéo hbh)
=> OM là đường trung bình của tg ADH => OM = 1/2 AH
bạn giúp mình bài tập này với
1. phân tích đa thức thành nhân tử
a) 5x(3 - 2x) - 7 (2x - 3)
b) x^3 - 4x^2 + 4x
c) x^2 + 5x + 6
2. cho biểu thức : M= (4x + 3) ^2 - 2x (x + 6) - 5 (x - 2) (x + 2)
a. rút gọn M
b. chứng minh M luôn dương.
( bạn cg giúp mình nhá. mình cảm ơn trc )