Bài: Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K lần lượt là hình chiếu của H trên AB, AC.
a)Tính S tam giác AIK biết AB=3cm, AC=5cm
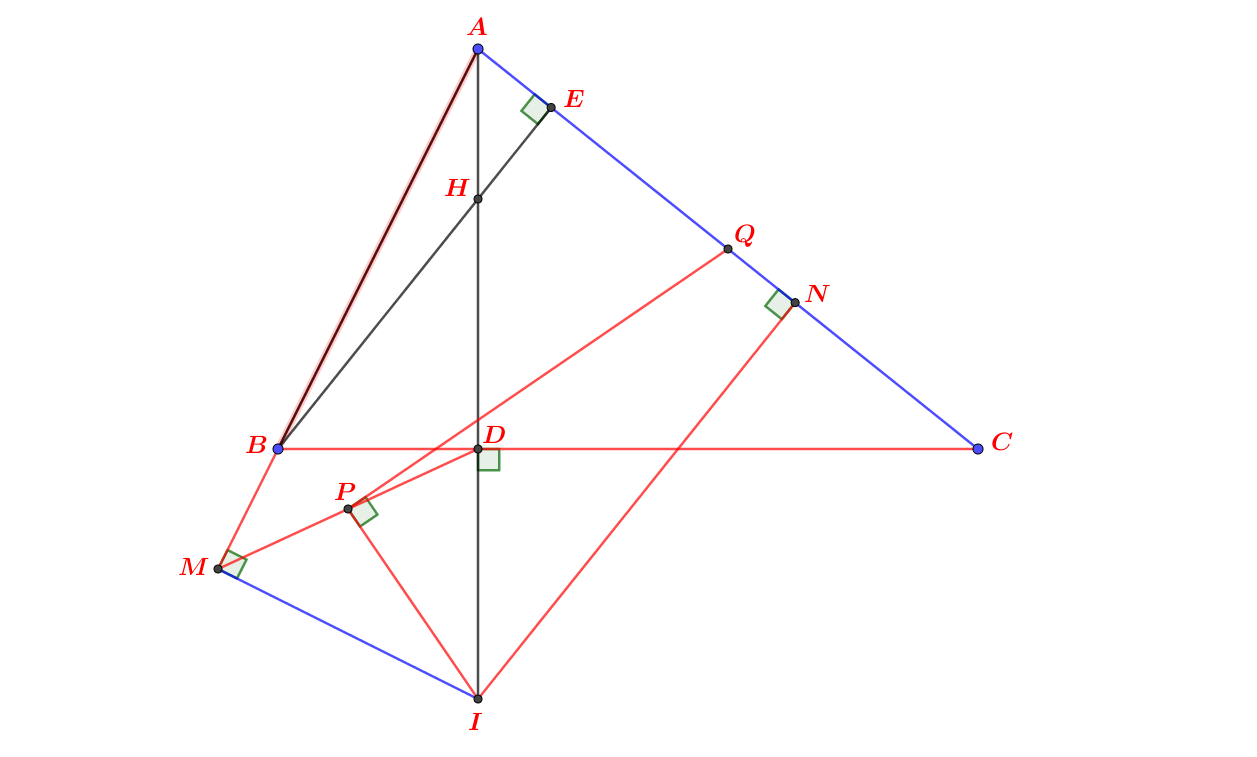
b) Gọi E đối xứng với H qua AB. Đường thẳng vuông góc với BC tại B cắt AE tại M. Chứng minh IK, AH, CM đồng quy
Giúp mình vs ạ :)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 5 2023
a: góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hcn
b: ΔHAB vuông tại H có HE vuông góc AB
nên AE*AB=AH^2
ΔAHC vuông tại H có HF vuông góc AC
nên AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
ΔACB
13 tháng 10 2022
a: \(AB=\sqrt{3\cdot15}=3\sqrt{5}\left(cm\right)\)
\(AC=\sqrt{12\cdot15}=6\sqrt{5}\left(cm\right)\)
b: \(\dfrac{HF}{HE}=\dfrac{AE}{AF}=\dfrac{AH^2}{AB}:\dfrac{AH^2}{AC}=\dfrac{AC}{AB}=2\)
=>HF=2HE
23 tháng 10 2021
a, Áp dụng HTL: \(BC=\dfrac{AB^2}{BH}=18\left(cm\right)\)
Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=9\sqrt{3}\left(cm\right)\)
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{9\cdot9\sqrt{3}}{18}=\dfrac{9\sqrt{3}}{2}\left(cm\right)\)
b, Áp dụng HTL: \(\left\{{}\begin{matrix}AB\cdot AE=AH^2\\AC\cdot AF=AH^2\end{matrix}\right.\Rightarrow AB\cdot AE=AC\cdot AF\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AF}{AE}\)
Mà góc A chung nên \(\Delta AEF\sim\Delta ACB\left(c.g.c\right)\)
Do đó \(\widehat{AEF}=\widehat{ACB}\)
a) -Sửa đề: \(AC=4cm\) (sửa lại cho số được đẹp)
-△ABC vuông tại A có: \(BC^2=AB^2+AC^2\).
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
△ACH và △BCA có: \(\widehat{AHC}=\widehat{BAC};\widehat{BCA}\) là góc chung.
\(\Rightarrow\)△ACH∼△BCA (g-g)
\(\Rightarrow\dfrac{CH}{CA}=\dfrac{AC}{BC}\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{4^2}{5}=3,2\left(cm\right)\).
△ABC có: IH//BC (cùng vuông góc AB).
\(\Rightarrow\dfrac{AI}{AB}=\dfrac{CH}{CB}\Rightarrow AI=\dfrac{AB.CH}{CB}=\dfrac{3.3,2}{5}=1,92\left(cm\right)\).
-Tứ giác AIHK có: \(\widehat{IAK}=\widehat{AIH}=\widehat{AKH}=90^0\).
\(\Rightarrow\)AIHK là hình chữ nhật \(\Rightarrow\widehat{AKI}=\widehat{CAH}\).
\(\widehat{CAH}=90^0-\widehat{ACB}=\widehat{ABC}\Rightarrow\widehat{AKI}=\widehat{ABC}\).
-△AIK và △ACB có: \(\widehat{AKI}=\widehat{ABC};\widehat{BAC}\) là góc chung.
\(\Rightarrow\)△AIK∼△ACB (g-g).
\(\Rightarrow\dfrac{S_{AIK}}{S_{ACB}}=\left(\dfrac{AI}{AC}\right)^2=\left(\dfrac{1,92}{4}\right)^2=0,2304\)
\(\Rightarrow S_{AIK}=0,2304.S_{ABC}=0,2304.\dfrac{1}{2}.3.4=1,3824\left(cm^2\right)\)
b) *CM cắt AH tại D, BM cắt AC tại F.
AH⊥BC tại H, BM⊥BC tại B \(\Rightarrow\)AH//BM.
E đối xứng với H qua AB \(\Rightarrow\widehat{HAB}=\widehat{BAM}\)mà \(\widehat{HAB}=\widehat{ABM}\).
\(\Rightarrow\)\(\widehat{ABM}=\widehat{BAM}\) \(\Rightarrow\)△ABM cân tại M \(\Rightarrow AM=BM\)
\(\widehat{ABM}=\widehat{BAM}\Rightarrow\widehat{MAF}=\widehat{MFA}\) \(\Rightarrow\)△AMF cân tại M \(\Rightarrow AM=FM\).
\(\Rightarrow BM=FM\) nên M là trung điểm BC.
-△BCM có: DH//BM \(\Rightarrow\dfrac{DH}{BM}=\dfrac{DC}{MC}\).
-△FCM có: AD//FM \(\Rightarrow\dfrac{DA}{FM}=\dfrac{DC}{MC}=\dfrac{DH}{BM}\Rightarrow DA=DH\)
\(\Rightarrow\)D là trung điểm AH mà AIHK là hình chữ nhật.
\(\Rightarrow\)D là trung điểm IK.
-Vậy IK, AH, CM đồng quy tại D.