Đa thức f(x) = 2x3 - 5x2 + x - a chia hết cho x + 3. hãy tìm a
Cám ơn mọi người trước nhá.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
2
29 tháng 10 2021
\(2x^3+5x^2-2x+a=x\left(2x^2-x+1\right)+3\left(2x^2-x+1\right)-3+a\)
\(=\left(2x^2-x+1\right)\left(x+3\right)-3+a⋮\left(2x^2-x+1\right)\)
\(\Rightarrow-3+a=0\Rightarrow a=3\)
29 tháng 10 2021
\(2x^3+5x^2-2x+a⋮2x^2-x+1\)
\(\Leftrightarrow2x^3-x^2+x+6x^2-3x+3+a-3⋮2x^2-x+1\)
\(\Leftrightarrow a-3=0\)
hay a=3
21 tháng 12 2022
a: Khi x=-1 thì B=2*(-1)^2+1+1=4
b: Để A chia hết cho B thì
\(2x^3-x^2+x+6x^2-3x+3+a-3⋮2x^2-x+1\)
=>a-3=0
=>a=3
c: Để B=1 thì 2x^2-x=0
=>x=0 hoặc x=1/2
16 tháng 10 2016
Đặt phép chia ta thấy A(x) chia cho B(x) được x^2-2x-1/2 và dư m-3/2
Để A(x) chia hết cho B(x) thì m-3/2=0 <=> m=3/2
(bạn biết cách chia đa thức một biến rồi chứ)
NT
1
14 tháng 4 2021
a) Ta có: B(x)-M(x)=A(x)
nên M(x)=B(x)-A(x)
\(=x^4-2x^3+5x^2+x+10-x^4-2x^3+5x^2+3x+6\)
\(=-4x^3+10x^2+4x+16\)
AH
Akai Haruma
Giáo viên
8 tháng 5 2022
Lời giải:
a.
\(C(x)=A(x)+B(x)=(2x^3-3x^2-x+1)+(-2x^3+3x^2+5x-2)\)
\(=(2x^3-2x^3)+(-3x^2+3x^2)+(-x+5x)+(1-2)=4x-1\)
b.
$C(x)=4x-1=0$
$\Rightarrow x=\frac{1}{4}$
Vậy $x=\frac{1}{4}$ là nghiệm của $C(x)$
c.
\(D(x)=A(x)-B(x)=(2x^3-3x^2-x+1)-(-2x^3+3x^2+5x-2)\)
\(=2x^3-3x^2-x+1+2x^3-3x^2-5x+2\)
\(=4x^3-6x^2-6x+3\)
CM
8 tháng 11 2017
Lời giải
Ta có
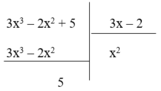
Vì phần dư R = 5 ≠ 0 nên phép chia đa thức 3 x 3 – 2 x 2 + 5 cho đa thức 3x – 2 là phép chia có dư. Do đó (I) sai
Lại có
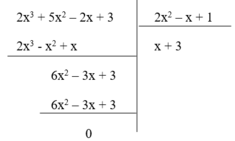
Nhận thấy phần dư R = 0 nên phép chia đa thức ( 2 x 3 + 5 x 2 – 2x + 3) cho đa thức (2 x 2 – x + 1) là phép chia hết. Do đó (II) đúng
Đáp án cần chọn là: D
2 tháng 11 2021
a, Để \(P\left(x\right)⋮Q\left(x\right)\Leftrightarrow P\left(-\dfrac{1}{2}\right)=\dfrac{1}{16}-\dfrac{5}{4}-2+a=0\Leftrightarrow a=\dfrac{51}{16}\)
b, \(n^3+6n^2+8n=n\left(n^2+6n+8\right)=n\left(n+2\right)\left(n+4\right)\)
Với n chẵn thì 3 số này là 3 số chẵn lt nên chia hết cho \(2\cdot4\cdot6=48\)
2 tháng 11 2021
https://meet.google.com/zvs-pdqd-skj?authuser=0&hl=vi. vào link ik
Vì f(x) chia hết cho x+3 nên ta có thể viết \(f\left(x\right)=2x^3-5x^2+x-a=\left(x+3\right).Q\left(x\right)\Rightarrow f\left(-3\right)=-102-a=0\Rightarrow a=-102\)
Xét phép chia (2x3-5x2+x-a) : (x+3)
f(x)=(2x3-5x2+x-a) chia hết cho (x+3) nếu tồn tại đa thức q(x) sao cho f(x)=(x+3).q(x)
Ta có: f(-3)=2.(-3)3-5.(-3)2+(-3)-a=(-3+3).q(x)
=>-102-a=0=>a=-102
Vậy a=-102 thì.................