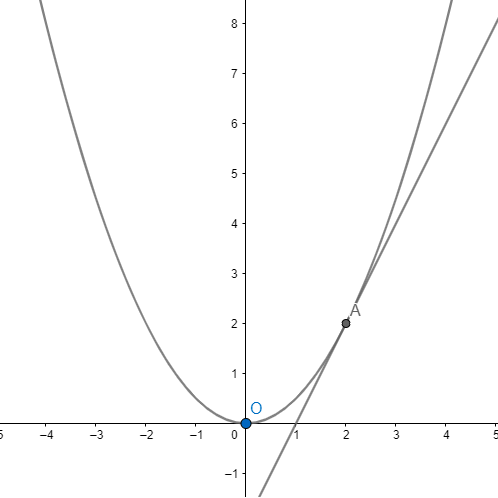
Cho đồ thị hàm số y = \(\dfrac{1}{2}x^2\) có đồ thị (P): y = x - 2 m. Vẽ đồ thị (P) tìm tất cả các giá trị của M sao cho (d) cắt (P) tại điểm có hoành độ bằng -1.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 10 2018
Đáp án B
Lấy đối xứng đồ thị hàm số f(x)(x-1) qua trục Ox ta được đồ thị của hàm số f x x - 1 . Từ đồ thị hàm số f x x - 1 ta thấy đường thẳng y = m 2 - m cắt hàm số f x x - 1 tại 2 điểm nằm ngoài [-1;1]
⇔ m 2 - m > 0 ⇔ [ m < 0 m > 1
CM
19 tháng 1 2018
Đáp án B
Lấy đối xứng đồ thị hàm số f ( x ) ( x − 1 ) qua trục Ox ta được đồ thị của hàm số f ( x ) x − 1 . Từ đồ thị hàm số f ( x ) x − 1 ta thấy đường thẳng y = m 2 − m cắt hàm số f ( x ) x − 1 tại 2 điểm nằm ngoài [ − 1 ; 1 ] ⇔ m 2 − m > 0 ⇔ m < 0 m > 1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1 2022
Pt hoành độ giao điểm:
\(\sqrt{2x^2-2x-m}-x-1=0\)
\(\Leftrightarrow\sqrt{2x^2-2x-m}=x+1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\2x^2-2x-m=x^2+2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x^2-4x-1=m\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb \(x\ge-1\)
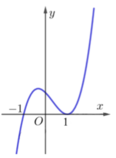
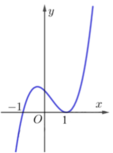
Từ đồ thị hàm \(y=x^2-4x-1\) ta thấy \(-5< m\le4\)
9 tháng 2 2021
a, - Ta có : Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 6 .
\(\Rightarrow-\dfrac{b}{a}=-\dfrac{3}{a}=6\)
\(\Rightarrow a=-\dfrac{1}{2}\)
b, - Xét phương trình hoành độ giao điểm :\(3x+2=\left(2m-1\right)x+8\)
\(\Leftrightarrow3x+2=2mx-x+8\)
\(\Leftrightarrow3x+2-2mx+m-8=0\)
\(\Leftrightarrow x\left(3-2m\right)=6-m\)
- Để hai đường thẳng cắt được nhau thì : \(3-2m\ne0\)
\(\Leftrightarrow m\ne\dfrac{3}{2}\)
Vậy ...
9 tháng 2 2021
a) Vì đồ thị hàm số y=ax+3 cắt trục hoành tại điểm có hoành độ bằng 6 nên
Thay x=6 và y=0 vào hàm số y=ax+3, ta được:
\(6a+3=0\)
\(\Leftrightarrow6a=-3\)
hay \(a=-\dfrac{1}{2}\)
Vậy: \(a=-\dfrac{1}{2}\)
b)
Để hàm số y=(2m-1)x+8 là hàm số bậc nhất thì \(2m-1\ne0\)
\(\Leftrightarrow2m\ne1\)
hay \(m\ne\dfrac{1}{2}\)(1)
Để (d) cắt (d') thì \(2m-1\ne3\)
\(\Leftrightarrow2m\ne4\)
hay \(m\ne2\)(2)
Từ (1) và (2) suy ra \(m\notin\left\{\dfrac{1}{2};2\right\}\)
