cho góc xOy vuông lấy A nằm trong góc đó gọi D là ddiiemr đối xứng của A qua Oy gọi B là điểm đối xứng của A qua Ox . Chúng minh rằng B đối xứng với D qua O
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 3 2017
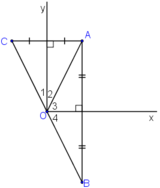
+ B đối xứng với A qua Ox
⇒ Ox là đường trung trực của AB
⇒ OA = OB (1)
+ C đối xứng với A qua Oy
⇒ Oy là đường trung trực của AC
⇒ OA = OC (2)
Từ (1) và (2) suy ra OB = OC (*).
+ Xét ΔOAC cân tại O (do OA = OC) có Oy là đường trung trực
⇒ Oy đồng thời là đường phân giác
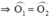
Xét ΔOAB cân tại O có Ox là đường trung trực
⇒ Ox đồng thời là đường phân giác
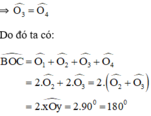
⇒ B, O, C thẳng hàng (**)
Từ (*) và (**) suy ra O là trung điểm BC
⇒ B đối xứng với C qua O.
11 tháng 10 2018
P.s: hình viết thiếu điểm A :))
Vì A và B đối xứng với nhau qua Ox => Ox là trung trực của AB
=> OB = OA (1)
C/m tương tự cũng có OA = OC (2)
Từ (1) và (2) => OB = OC => B và C đối xứng với nhau qua O ( đpcm )
HH
1 tháng 7 2020
( vào TKHĐ là thấy hình )
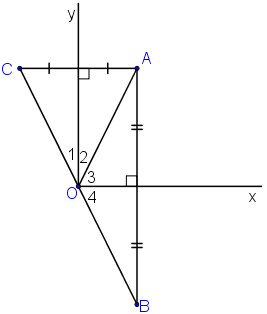
+ B đối xứng với A qua Ox
=> Ox là đường trung trực của AB
=> OA = OB (1)
+ C đối xứng với A qua Oy
=> Oy là đường trung trực của AC
=> OA = OC (2)
Từ (1) và (2) suy ra OB = OC (*).
+ Xét ΔOAC cân tại O (do OA = OC) có Oy là đường trung trực
=> Oy đồng thời là đường phân giác
\(\Rightarrow\widehat{O_1}=\widehat{O_2}\)
Xét ΔOAB cân tại O có Ox là đường trung trực
=> Ox đồng thời là đường phân giác
\(\Rightarrow\widehat{O_3}=\widehat{O_4}\)
Từ đó ta có :
\(\widehat{BOC}=\widehat{O_1}+\widehat{O_2}+\widehat{O_3}+\widehat{O_4}\)
\(=2.\widehat{O_2}+2.\widehat{O_3}=2.\left(\widehat{O_2}+\widehat{O_3}\right)\)
\(=2.\widehat{xOy}=2.90^o=180^o\)
=> B, O, C thẳng hàng (**)
Từ (*) và (**) suy ra O là trung điểm BC
=> B đối xứng với C qua O.
9 tháng 11 2021
a: Ta có: B đối xứng với A qua Ox
nên OA=OB(1)
Ta có: C đối xứng với A qua Oy
nên OA=OC(2)
Từ (1) và (2) suy ra OB=OC
CM
18 tháng 9 2017
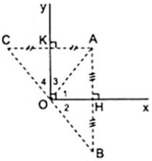
Vẽ AH ⊥ Ox, AK ⊥ Oy
Vẽ hai điểm B, C sao cho H, K lần lượt là trung điểm của AB, AC thì B là điểm đối xứng với A qua Ox, C là điểm đối xứng với A qua Oy.
Vì O ∈ Ox, O ∈ Oy nên O đối xứng với O qua Ox, Oy.
Áp dụng tính chất của phép đối xứng ta được
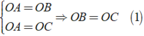
Và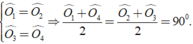
⇒ B O C ^ = 180 0 . ( 2 )
Từ ( 1 ), ( 2 ) suy ra O là trung điểm của BC hay B đối xứng với C qua O.
21 tháng 4 2017
54. Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, gọi C là điểm đối xứng với A qua Oy. Chứng mình rằng điểm B đối xứng với điểm C qua O.
Bài giải:
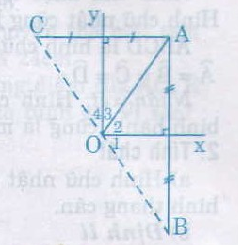
Cách 1:
B đối xứng với A qua Ox nên Ox là đường trung trực của AB => OA = OB
C đối xứng với A qua Oy nên OY là đường trung trực của AC => OA = OC
Suy ra OB = OC (1)
∆AOB cân tại O =>ˆO1O1^ = ˆO2O2^ = ˆAOB2AOB2^
∆AOC cân tại O =>ˆO3O3^ = ˆO4O4^ = ˆAOC2AOC2^ˆAOBAOB^ˆAOCAOC^
Mà widehatAOBwidehatAOB + ˆAOCAOC^ = 2(ˆO2O2^ + ˆO3O3^) = 2.900 = 1800
=> B, O, C thẳng hàng (2)
Từ (1) và (2) suy ra B đối xứng với C qua O.
Cách 2:
A đối xứng với B qua Ox và O nằm trên Ox nên OA đối xứng với OB qua OX suy ra
OA = OB.
A đối xứng với C qua Oy và O nằm trren Oy nên OA đối xứng với OC qua Oy.
Suy ra OA = OC
Do đó OB = OC (1)
và ˆAOBAOB^ + ˆAOCAOC^ = 2(ˆO2O2^ + ˆO3O3^) = 2.900 = 1800
=>B, O, C thẳng hàng (2)
Từ (1) và (2) suy ra B đối xứng với C qua O.
CM
5 tháng 6 2019
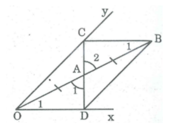
Xét ∆ OAD và ∆ BAC, ta có:
OA = AB (tính chất đối xứng tâm)
∠ A 1 = ∠ A 2 (đối đỉnh)
∠ O 1 = ∠ B 1 (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua A.
13 tháng 10 2021
+ B đối xứng với A qua Ox
⇒ Ox là đường trung trực của AB
⇒ OA = OB (1)
+ C đối xứng với A qua Oy
⇒ Oy là đường trung trực của AC
⇒ OA = OC (2)
Từ (1) và (2) suy ra OB = OC (*).
+ Xét ΔOAC cân tại O (do OA = OC) có Oy là đường trung trực
⇒ Oy đồng thời là đường phân giác
Xét ΔOAB cân tại O có Ox là đường trung trực
⇒ Ox đồng thời là đường phân giác
⇒ B, O, C thẳng hàng (**)
Từ (*) và (**) suy ra O là trung điểm BC
⇒ B đối xứng với C qua O.
13 tháng 10 2021
AA đối xứng với BB qua OxOx và OO nằm trên OxOx nên OAOA đối xứng với OBOB qua OxOx suy ra OA=OBOA=OB. (1)
Tam giác AOBAOB cân tại OO nên ˆO1=ˆO2O^1=O^2 (3)
AA đối xứng với CC qua OyOy và OO nằm trên OyOy nên OAOA đối xứng với OCOC qua OyOy suy ra OA=OCOA=OC (2)
Quảng cáo
Tam giác AOCAOC cân tại OO nên ˆO3=ˆO4O^3=O^4 (4)
Từ (1) và (2) suy ra OB=OCOB=OC (*)
Từ (3) và (4) suy ra ˆO1+ˆO2+ˆO3+ˆO4=2(ˆO2+ˆO3)=2.900=1800O^1+O^2+O^3+O^4=2(O^2+O^3)=2.900=1800
Do đó B,O,CB,O,C thẳng hàng (2*)
Từ (*) và (2*) suy ra BB đối xứng với CC qua OO.
3 tháng 12 2021
Gọi giao điểm của MN và Ox là điểm A; giao điểm của MN và Oy là điểm B.
Ta có: N là điểm đối xứng với M qua Ox (gt).
O \(\in\) Ox.
=> \(\left\{{}\begin{matrix}OA\perp MN.\\\text{ON = OM.(1)}\end{matrix}\right.\)
Ta có: P là điểm đối xứng với M qua Oy (gt).
O \(\in\) Oy.
=> \(\left\{{}\begin{matrix}OB\perp MP.\\\text{OM = OP.(2)}\end{matrix}\right.\)
Từ (1) và (2) => OP = ON = OM.
Xét tam giác NOM có: ON = OM (cmt).
=> Tam giác NOM cân tại O.
Mà OA là đường cao (do OA vuông góc MN).
=> OA là phân giác của ^NOM (Tính chất các đường trong tam giác cân).
=> ^NOA = ^AOM.
Xét tam giác MOP có: OP = OM (cmt).
=> Tam giác MOM cân tại O.
Mà OB là đường cao (do OB vuông góc MP).
=> OB là phân giác của ^MOP (Tính chất các đường trong tam giác cân).
=> ^MOB = ^BOP.
Ta có: ^NOA + ^AOM + ^MOB + ^BOP.
= 2. ^AOM + 2. ^MOB.
= 2. (^AOM + ^MOB).
= 2. ^AOB.
= 2. 90o = 180o.
=> 3 điểm N; O; P thẳng hàng.
Mà OP = ON (cmt).
=> O là trung điểm của NP.
=> P và N đối xứng nhau qua O (đpcm).
B đối xứng với C qua OX thì sao lại chứng minh B đối xứng với C qua o???
Nếu B đối xứng với A qua OX thì chứng minh dễ ợt
Vì O đx với A qua Oy=>OC=OA, tam giác COA cân tại A lại có Oy là trung trực =>OY là phân giác=>góc COy=góc AOy
chứng minh tương tự =>OA=Ob và góc AOx=BOy
vì Aox+Aoy=xoy=90 độ=>COB=2xoy=2.90=180 độ=>C,O,B thẳng hàng
và OC=Ob=> B đx với C qua O
C ở đâu vậy bạn bạn có nhầm ko