bài 3. viết vào chỗ chấm cho thích hợp :
a. bốn đỉnh là ..................
b. bốn cạch AB,BC,CD,AD đều ............
c. hai đường chéo AC và BD .............. với nhau và cắt nhau ở .......................... của mỗi đường
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Từ ĐKĐB dễ thấy các tứ giác ABID,ABCK là hình bình hành do có các cặp cạnh đối song song với nhau
\(\Rightarrow AB=DI;AB=CK\Rightarrow DI=CK\Rightarrow DK=CI\)
Áp dụng định lý Ta-lét:
\(AB||DK\Rightarrow\frac{DE}{EB}=\frac{DK}{AB}\)
\(AB||CI\Rightarrow\frac{IF}{FB}=\frac{CI}{AB}\)
Maf \(CI=DK\)(cmt)
\(\Rightarrow\frac{DE}{EB}=\frac{IF}{FB}\)Theo định lý Ta-let đảo suy ra EF\(||\)CD
b)Từ các đường thẳng song song, và DI=CK=AB, áp dụng định lý Ta-let:
\(\frac{AB}{EF}=\frac{DI}{EF}=\frac{BD}{BE}=\frac{BE+ED}{BE}=1+\frac{ED}{BE}=1+\frac{DK}{AB}=1+\frac{CE-CK}{AB}=1+\frac{CD-AB}{AB}=\frac{CD}{AB}\)
\(\Rightarrow AB^2=EF.CD\)( đpcm )

Hướng dẫn giải:
Hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

a) Vẽ hình chữ nhật ABCD có chiều dài 4 cm, chiều rộng 3 cm. Sau đó nối đỉnh A với đỉnh C, đỉnh B, đỉnh D.
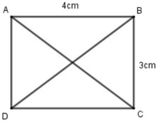
b) Đo chiều dài đoạn thẳng
AC, BD rồi viết số thích hợp vào chỗ chấm:
- AC = 5 cm
- BD = 5 cm
c) Nhận xét:
Độ dài AC = độ dài BD
(AC, BD là hai đường chéo của hình chữ nhật)
a: A,B,C,D
b: bằng nhau
c: vuông góc
trung điểm