Giúp e giải chỉ tiết câu 7 này đi ạ mình giải k ra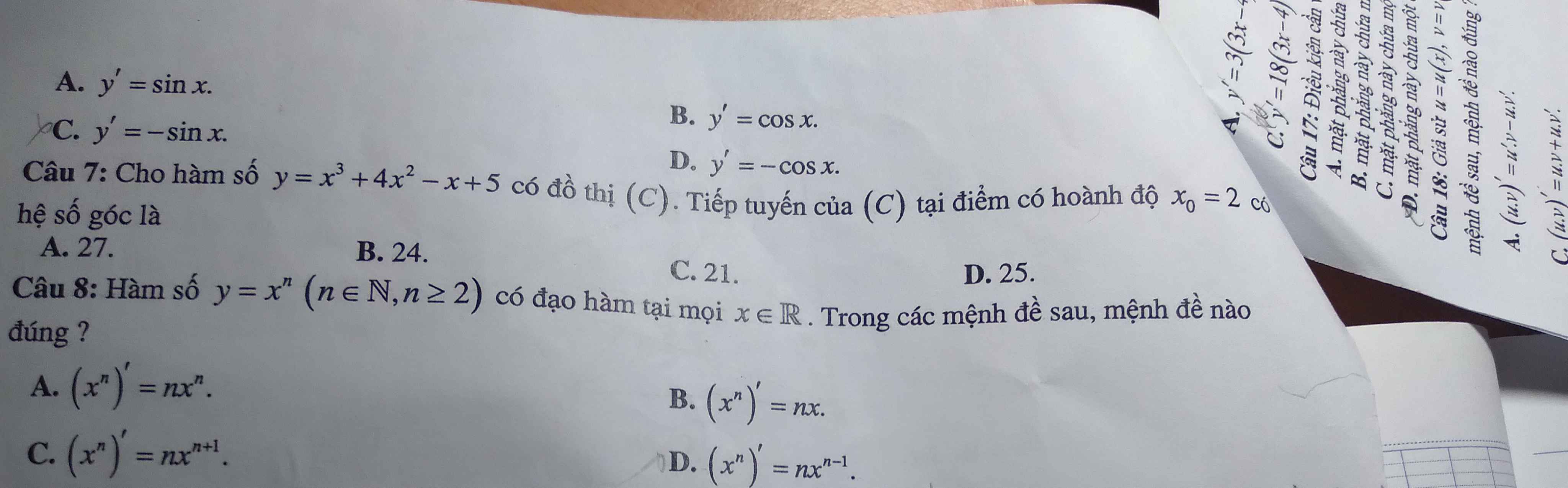
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2022
\(y=\left(x^7+x\right)^3\)
\(y'=3\left(x^7+x\right)^2.\left(x^7+x\right)'=3\left(x^7+x\right)^2\left(7x^6+1\right)\)
16 tháng 4 2022
Câu 11.
a)Độ tự cảm của ống dây:
\(L=4\pi\cdot10^{-7}\cdot\dfrac{N^2}{l}S=4\pi\cdot10^{-7}\cdot\dfrac{1000^2}{0,2}\cdot50\cdot10^{-4}=0,0314H=0,0314\cdot10^3=31,4mH\)
b)Độ biến thiên từ thông:
\(\Delta\Phi=L\cdot\Delta i=0,0314\cdot\left(1-0\right)=0,0314Wb\)
Suất điện động cảm ứng:
\(e_{tc}=\left|-\dfrac{\Delta\Phi}{\Delta t}\right|=\left|-\dfrac{0,0314}{0,1}\right|=0,314V\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
7.
\(y'=\left(-x^3\right)'-\left(5x\right)'+\left(2\right)'=-3x^2-5\)
\(y''=\left(-3x^2\right)'-\left(5\right)'=-6x\)
8.
\(\lim\limits_{x\rightarrow+\infty}\left(x^3+3x-2\right)=\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{3}{x^2}-\dfrac{2}{x^3}\right)\)
Do: \(\lim\limits_{x\rightarrow+\infty}x^3=+\infty\)
\(\lim\limits_{x\rightarrow+\infty}\left(1+\dfrac{3}{x^2}-\dfrac{2}{x^3}\right)=1>0\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{3}{x^2}-\dfrac{2}{x^3}\right)=+\infty\)
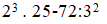
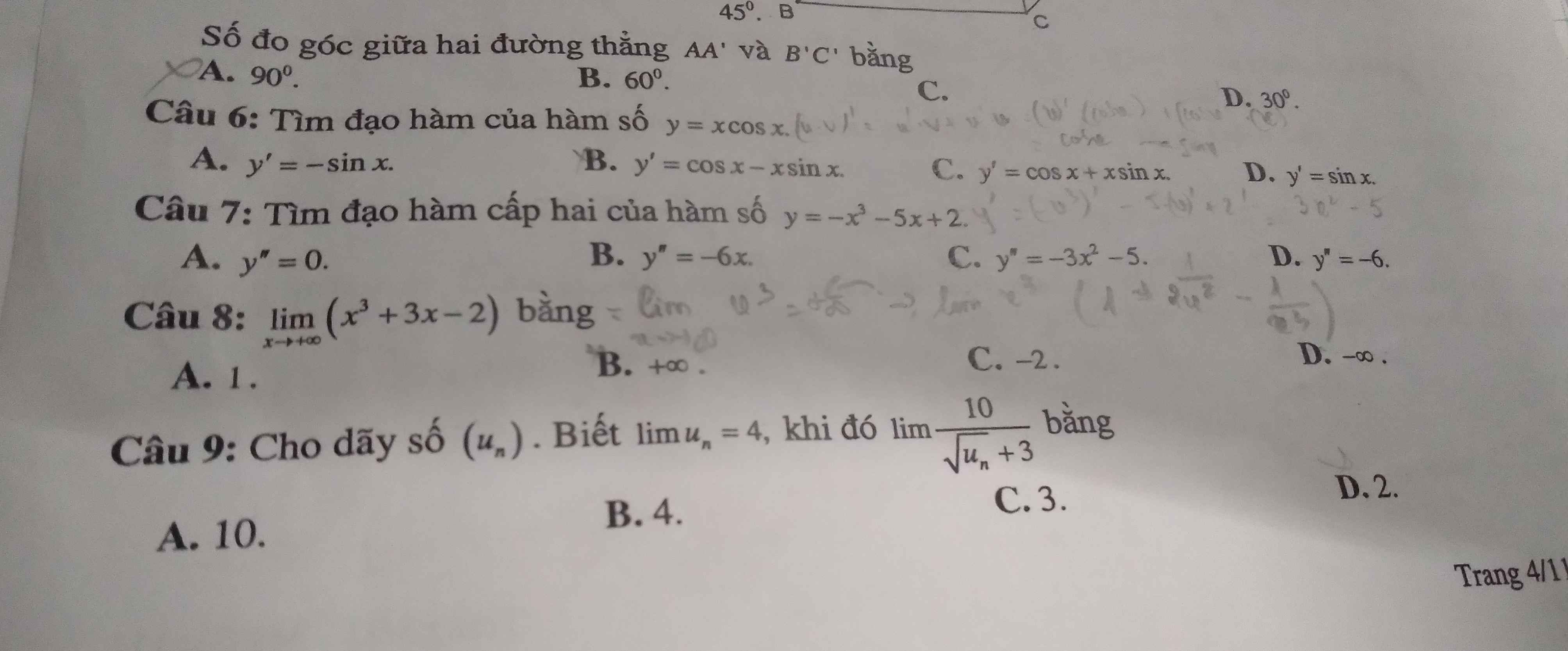
7.
\(y'=3x^2+8x-1\)
\(\Rightarrow y'\left(2\right)=3.2^2+8.2-1=27\)