Một thấu kính hội tụ mỏng đặt cố định. Người ta đặt một vật sáng AB phẳng và mỏng sao cho AB vuông góc với trục chính tại A. Ảnh của AB là ảnh thật A1B1. Sau đó di chuyển AB ra xa thấu kính thêm một đoạn 10 cm, sao cho A vẫn ở trên trục chính và AB vuông góc với trục chính thì thấy ảnh của AB di chuyển một đoạn 5 cm, và ảnh trước có chiều cao gấp 2 lần ảnh sau. Tìm khoảng cách từ quang tâm đến tiêu điểm chính của thấu kính. Giải bài toán bằng phương pháp hình học và bằng phương pháp sử dụng công thức thấu kính
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Gọi d 1 ; d 1 ' là khoảng cách từ vật đến thấu kính, từ ảnh đến thấu kính trước khi di chuyển.
+ Gọi d 2 ; d 2 ' là khoảng cách từ vật đến thấu kính, từ ảnh đến thấu kính sau khi di chuyển.
+ Ảnh thật cao gấp 2 lần vật nên:
![]()
+ Di chuyển thấu kính râ xa thêm 15 cm nên ta có:
![]()
+ Thấu kính dịch ra xa vật thì ảnh dịch lại gần thấu kính. Vì thấu kính rời lại gần màn thêm 15 cm đồng thời màn cũng dời lại gần thấu kính thêm 15 cm nên:
![]()
Thay (1) và (2) vào ta có:
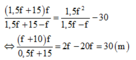
=> Chọn A.


+ Thấu kính dịch ra xa vật thì ảnh
dịch lại gần thấu kính. Vì thấu kính rời lại gần màn thêm 15 cm đồng thời màn cũng dời lại gần thấu kính thêm 15 cm nên:


Chọn đáp án A
+ Khi chưa dịch vật ta có: 1 d + 1 d ' = 1 f = 1 12
+ Khi đó ảnh là ảnh ảo nên d ' < 0 và nằm trước thấu kính => Sau khi dịch vật thì cho ảnh thật => nằm sau thấu kính và cách thấu kính một đoạn bằng 72 + d ' d o d ' < 0
Vậy ta có: 1 d + 8 + 1 d ' + 72 = 1 f = 1 12
Kết hợp hai phương trình trên giải hệ ta thu được:
d ' = d f d − f = 12 d d − 12 ⇒ 1 d + 8 + 1 12 d d − 12 = 1 12 ⇒ d = 8 c m

Chọn đáp án A
+ Khi chưa dịch vật ta có:
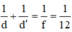
+ Khi đó ảnh là ảnh ảo nên ![]() và nằm trước thấu kính => Sau khi dịch vật thì cho ảnh thật => nằm sau thấu kính và cách thấu kính một đoạn bằng
và nằm trước thấu kính => Sau khi dịch vật thì cho ảnh thật => nằm sau thấu kính và cách thấu kính một đoạn bằng ![]()
Vậy ta có:
![]()
Kết hợp hai phương trình trên giải hệ ta thu được:
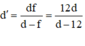
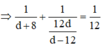
![]()
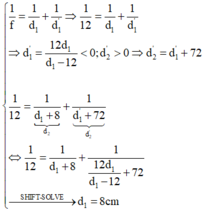
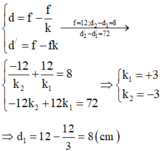
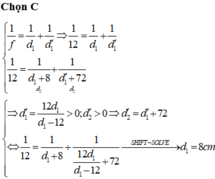



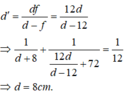
giúp đi