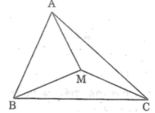
Cho điểm M nằm trong tam giác ABC. 1) So sánh AB với MA + MB . 2) CMR: AB + AC + BC < 2(MA + MB + MC) . 3) Chứng minh rằng MA + MB +MC lớn hơn nửa chu vi tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 3 2019
Trong ΔAMB, ta có:
MA + MB > AB (bất đẳng thức tam giác) (1)
Trong ΔAMC, ta có:
MA + MC > AC (bất đẳng thức tam giác) (2)
Trong ΔBMC, ta có:
MB + MC > BC (bất đẳng thức tam giác) (3)
Cộng từng vế (1), (2) và (3), ta có:
MA + MB + MA + MC + MB + MC > AB + AC + BC
⇔ 2(MA + MB + MC) > AB + AC + BC
Vậy MA + MB + MC > (AB + AC + BC) / 2
TP
Thảo Phương
CTVVIP
20 tháng 7 2017
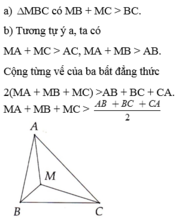
(h.45) Xét \(\Delta ABM:\)MA+MB>AB (1)
Xét \(\Delta AMC:\) MA+MC>AC (2)
Xét \(\Delta BMC:\) MB+MC>BC (3)
Cộng từng vế (1), (2), (3):
2(MA+MB+MC)>\(\text{AB+AC+BC}\)
Suy ra :
MA+MB+MC>\(\dfrac{\text{AB+AC+BC}}{2}\)
26 tháng 3 2022
a) Xét ΔBMC ta có: MB + MC > BC (bất đẳng thức tam giác)
b)
*Xét ΔABM ta có: AM + BM > AB (1)
*Xét ΔACM ta có: AM + CM > AC (2)
*Xét ΔBMC ta có: BM + CM > BC (3)
Từ (1); (2); (3)
=> AM + BM + AM + CM + BM + CM > AB + AC + BC
=> 2. AM + 2. BM + 2. CM > AB + AC + BC
=> 2. (AM + BM + CM) > AB + AC + BC
Hay: 2. (MA + MB + MC) > AB + BC + CA
26 tháng 3 2022
c)Gọi I là giao điểm của BM và AC.
Áp dụng bất đẳng thức tam giác vào ΔIMC ta có: MC<MI+IC (1)
Cộng MB vào hai vế (1) ta được: MC+MB<MI+IC+MB
⇒MC+MB<MI+MB+IC
⇒MC+MB<IB+IC (2)
d)Áp dụng bất đẳng thức tam giác vào ΔIBA ta có: IB<IA+AB (3)
Cộng IC vào hai vế (3) ta được: IB+IC<IA+AB+IC
⇒ IB+IC<IA+IC+AB
⇒IB+IC<AC+AB (4)
e)Từ (2) và (4) suy ra MB+MC<AB+AC
f)Áp dụng bđt tam giác, ta có:
AB+AI > BI = MB+MI, CI + MI > MC
=> AB + AI + CI + MI > MB + MI + MC
Mà AI + CI = AC
=> AB + AC > MB + MC [1]
Áp dụng bđt tam giác, ta cũng có:
BA + BC > MA + MC [2],
CA + CB > MA + MB [3]
Từ [1][2][3] => 2 (AB+AC+CA) > MA + MB + MC
=> MA + MB + MC < AB + AC + BC (đpcm)
26 tháng 3 2022
a) Xét ΔBMC ta có: MB + MC > BC (bất đẳng thức tam giác)
b)
*Xét ΔABM ta có: AM + BM > AB (1)
*Xét ΔACM ta có: AM + CM > AC (2)
*Xét ΔBMC ta có: BM + CM > BC (3)
Từ (1); (2); (3)
=> AM + BM + AM + CM + BM + CM > AB + AC + BC
=> 2. AM + 2. BM + 2. CM > AB + AC + BC
=> 2. (AM + BM + CM) > AB + AC + BC
Hay: 2. (MA + MB + MC) > AB + BC + CA
c)Gọi I là giao điểm của BM và AC.
Áp dụng bất đẳng thức tam giác vào ΔIMC ta có: MC<MI+IC (1)
Cộng MB vào hai vế (1) ta được: MC+MB<MI+IC+MB
⇒MC+MB<MI+MB+IC
⇒MC+MB<IB+IC (2)
d)Áp dụng bất đẳng thức tam giác vào ΔIBA ta có: IB<IA+AB (3)
Cộng IC vào hai vế (3) ta được: IB+IC<IA+AB+IC
⇒ IB+IC<IA+IC+AB
⇒IB+IC<AC+AB (4)
e)Từ (2) và (4) suy ra MB+MC<AB+AC
f)Áp dụng bđt tam giác, ta có:
AB+AI > BI = MB+MI, CI + MI > MC
=> AB + AI + CI + MI > MB + MI + MC
Mà AI + CI = AC
=> AB + AC > MB + MC [1]
Áp dụng bđt tam giác, ta cũng có:
BA + BC > MA + MC [2],
CA + CB > MA + MB [3]
Từ [1][2][3] => 2 (AB+AC+CA) > MA + MB + MC
=> MA + MB + MC < AB + AC + BC (đpcm)
2 tháng 4 2016
áp dụng đ/lý bất đẳng thức ta có: MA < MI + IA
=> MA + MB < MI + IA + MB
=> MA + MB < IB + IA (1)
tương tự ta có: IB < IC + BC
=> IB + IA < IC + BC + IA
=> IB + IA < AC + BC (2)
từ (1) và (2) => MA + MB < AC + BC (3)
tương tự ta cũng có: MA + MC < AB + BC (4)
MB + MC < AB + AC (5)
cộng theo vế (3) ; (4) ; (5) ta có:
MA + MB + MA + MC + MB + MC < AC + BC+ AB + BC + AB + AC
2( MA + MB + MC) < 2( AB + AC + BC)
MA + MB + MC < AB + AC + BC ( vì cùng chia 2 vế cho 2) (6)
áp dụng đ/lý bất đẳng thức tam giác ta có:
AB < MA + MB
AC < MA + MC
BC < MC + MB
cộng theo vế của các bất đẳng thức trên ta có:
AB + AC + BC < MA + MB + MA + MC + MC + MB
AB + AC + BC < 2( MA + MB + MC)
AB + AC + BC / 2 MA + MB + MC ( chia cả 2 vế cho 2) (7)
từ (6) và (7) => AB + AC + BC / 2< MA + MB + MC < AB + AC + BC
vậy MA + MA + MC lớn hơn nửa chu vi và nhỏ hơn chu vi tam giác ABC
30 tháng 4 2019
Trong ΔAMB, ta có:
MA + MB > AB (bất đẳng thức tam giác) (1)
Trong ΔAMC, ta có:
MA + MC > AC (bất đẳng thức tam giác) (2)
Trong ΔBMC, ta có:
MB + MC > BC (bất đẳng thức tam giác) (3)
Cộng từng vế (1), (2) và (3), ta có:
MA + MB + MA + MC + MB + MC = AB + AC + BC
⇔ 2(MA + MB + MC) > AB + AC + BC
Vậy MA + MB + MC > (AB + AC + BC) / 2 .
MA
13 tháng 5 2015
ap dụng đinh lí bất dẳng thức tam giác ta cóMA<MI+IA
TA cộng cả 2 vế trên với MB ta có MA+MB<MI+MB+IA
MA+MB< IB +IA (1)
tương tự ta có IB<IC+BC
Cộng cả hai vế trên vớiIA ta có IB+IA<IC+IA+BC
IB+IA<AC+ BC(2)
từ (1) và (2) ta được MA+MB<IA+IB<AC+BC
hay MA+MB<AC+BC (3)
Tương tự như vậy ta cũng có MA+MC<AB+BC(4)
MB+MC<AB+AC (5)
CÔng theo vế của (3),(4).(5) ta được
MA+MB+MA+MC+MB+MC<AC+BC+AB+BC+AB+AC
2(MA+MB+MC)<2(AB+AC+BC)
MA+MB+MC<AC+AB+BC(cùng chia 2 vế cho 2)(**)
Aps dụng đ/l bất đẳng thức tam giác ta có
AB<MB+MA
AC<MA+MC
BC<MC+MB
cộng theo vế của các bất đảng thức trên ta được
AB+AC+BC<MB+MA+MA+MC+MC+MB
AB+AC+BC<2(MA+MB+MC)
AB+AC+BC/2<MA+MB+MC (CHIA CẢ HAI VẾ CHO 2) (*)
TỪ (**) VÀ (*) ta suy ra
AB+AC+BC/2<MA+MB+MC<AB+AC+BC
vậy MA+MB+MC lớn hơn nửa chu vi và nhỏ hơn chu vi cua tam giác ABC
ko nhìn thấy
là sao ?