Câu 4: Cho tam giác đều ABC , đường trung tuyến AM . Trên tia đối
tia CB lấy điểm D sao cho CD = CB. Vẽ CH 1 AD (He AD)
a) Chứng minh : H là trung điểm của AD
b) Chứng minh: AABD vuông tại A.
c) Tia đối tia CH và tia AM cắt nhau tại P. Chứng minh: Điểm C là trọng tâm
của tam giác APD.
d) Biết AB = 10 cm. Tính AM (ghi kết quả đúng không làm tròn số)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔCAD cân tại C
mà CH là đường cao
nên H là trung điểm của AD
b: Xét ΔABD có
AC là trung tuyến
AC=BD/2
=>ΔABD vuông tại A
c: Xét ΔAHC vuông tại H và ΔAMC vuông tại M có
AC chung
góc HAC=góc MAC
=>ΔAHC=ΔAMC
=>AH=AM
Xét ΔAHP vuông tại H và ΔAMD vuông tại M có
AH=AM
góc HAP chung
=>ΔAHP=ΔAMD
=>AP=AD
mà góc PAD=60 độ
nên ΔAPD đều
=>C là trọng tâm của ΔAPD

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

A^ + B^ = 90o (phụ nhau)
A^ + 2* A^=90o
3* A^ = 90o
A^= 30o
B^= 2* A^ =2* 30o = 60o
a)
Xét \(\Delta\)ACD và \(\Delta\)ACB:
ACD^ = ACB^= 90o
AC chung
CD =CB
=> \(\Delta\)ACD =\(\Delta\)ACB (2 cạnh góc vuông)
=> AD = AB(2 cạnh tương ứng)
Phải là :Trên AD lấy M, trên AB lấy N (AM = AN) chứ.
b)
\(\Delta\)ACD =\(\Delta\)ACB (cmt) => A1 =A2 (2 góc tương ứng)
Xét \(\Delta\)AMC và \(\Delta\)ANC:
AC chung
A1 =A2 (cmt)
AM =AN
=> \(\Delta\)AMC = \(\Delta\)ANC (c.g.c)
=> CM =CN (2 cạnh tương ứng)
c)
AD = AB (cmt) =. D^ = B^
D^ + B^ + DAB^ =180o
2* D^ +DAB^=180o
D^= \(\frac{180o-DAB}{2}\) (1)
Ta có: AM = AN => AMN^ = ANM^
AMN^ + ANM^ + DAB^ =180o
2* AMN^ + DAB = 180o
AMN^ = \(\frac{180o-DAB}{2}\) (2)
Từ (1) và (2) => D^ = AMN^
Mà D^ so le trong với AMN^ => MN // DB

giúp mik nhanh câu c dc khum ạ
2 câu kia mik xong r
cảm ơn các bạn

ta có AD=2 AM (gt)
-> M là trung điểm AD
Xét tam giac ABM và tam giác DCM ta có
BM = MC ( M là trung điểm BC)
AM=MD ( M là trung điểm AD)
góc AMB = góc CMD (2 góc đối dinh)
-> tam giác ABM = tam giác DCM (c-g-c)
-> góc ABC = góc DCB
b) ta có
góc ABC = góc DCB (cmt)
mà 2 góc nam o vi tri sole trong
nên AB//CD
mà AB vuông góc AC tại A ( tam giác ABC vuông tại A)
-> CD vuông góc AC
c) ACE là góc nào?



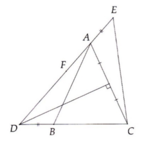
a: Xét ΔCAD có CA=CD
nên ΔCAD cân tại C
mà CH là đường cao
nên H là trung điểm của AD
b: Xét ΔABD có
AC là đường trung tuyến
AC=BD/2
DO đó: ΔABD vuông tại A