Giải nhanh giúp em với ạ em đang cần gấp lắm rồi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3:
a:Các tia trên hình là Ax,Ay,Bx,By,Cx,Cy
=>Có 6 tia
b: AB<AC
=>B nằm giữa A và C
=>AB+BC=AC
=>BC=4cm
c: AI=3/2=1,5cm
CI=7-1,5=5,5cm

Câu 3:
\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m^2-3m+4\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-3m+4\right)\)
\(=4m^2-16m+4-4m^2+12m-16=-4m-12\)
Để phương trình có hai nghiệm phân biệt thì -4m-12>0
=>-4m>12
hay m<-3
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-3m+4\end{matrix}\right.\)
Theo đề, ta có: \(x_1+x_2=x_1x_2\)
\(\Leftrightarrow m^2-3m+4-2m+2=0\)
=>(m-2)(m-3)=0
hay \(m\in\varnothing\)


Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 9: B


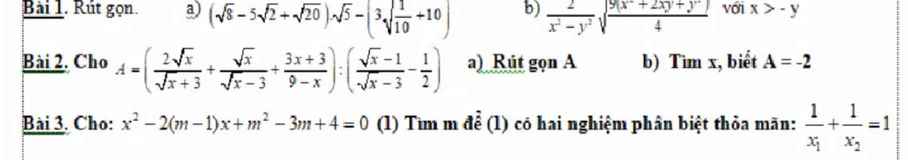





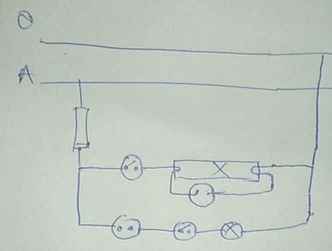
 ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn



Bài 5:
\(x^2+y^2+1\ge xy+x+y\)
\(\Leftrightarrow2\left(x^2+y^2+1\right)\ge2\left(xy+x+y\right)\)
\(\Leftrightarrow2x^2+2y^2+2\ge2xy+2x+2y\)
\(\Leftrightarrow2x^2+2y^2+2-2xy-2x-2y\ge0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2-2x+1\right)+\left(y^2-2y+1\right)\ge0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-1\right)^2+\left(y-1\right)^2\ge0\left(đúng\right)\)
-Dấu bằng xảy ra \(\Leftrightarrow x=y=1\)