Giải giúp mình gấp câu b, c với. Mình đang cần gấp. Mình cảm ơn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=\dfrac{2\sqrt{x}+1+\left(1-\sqrt{x}\right)\left(1+\sqrt{x}\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}+1+1-x}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{\sqrt{x}+2}=\dfrac{-x+2\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}=\dfrac{-x+2\sqrt{x}+2}{x+3\sqrt{x}+2}\)


Bài 3:
a: Gọi OK là khoảng cách từ O đến AB
Suy ra: K là trung điểm của AB
hay \(AK=BK=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔOKA vuông tại K, ta được:
\(OA^2=OK^2+KA^2\)
hay OK=3(cm)

a: Xét ΔSBM và ΔSNB có
\(\widehat{SBM}=\widehat{SNB}\)
\(\widehat{BSM}\) chung
Do đó: ΔSBM\(\sim\)ΔSNB
Suy ra: SB/SN=SM/SB
hay \(SB^2=SM\cdot SN\)
b: Xét (O) có
SA là tiếp tuyến
SB là tiếp tuyến
Do đó: SA=SB
mà OA=OB
nên SO là đường trung trực của AB
=>SO⊥AB
Xét ΔOBS vuông tại B có BH là đường cao
nên \(SH\cdot SO=SB^2=SM\cdot SN\)



\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-1\end{matrix}\right.\)
8: \(=\dfrac{x_1^2+x_2^2}{\left(x_1\cdot x_2\right)^2}=\dfrac{2}{1}=2\)
9: \(=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=2^3-3\cdot\left(-1\right)\cdot2=8+6=14\)
16: \(=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{2^2-4\cdot\left(-1\right)}=\sqrt{4+4}=2\sqrt{2}\)

(27 + 29) + (86 - 84) + 5
= 56 + 2 + 5
= 63
Chúc bạn học tốt!! ^^
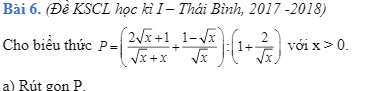

 , mình đang cần giải gấp. Cảm ơn mn nhiều.
, mình đang cần giải gấp. Cảm ơn mn nhiều.


 Mình đang cần rất gấp từ câu 7 đến câu 21. Mọi người giải giúp mình. Mình cảm ơn !
Mình đang cần rất gấp từ câu 7 đến câu 21. Mọi người giải giúp mình. Mình cảm ơn !