Một ca nô chạy xuôi dòng từ bến A đến bến B rồi ngay lập tức quay trở lại A hết tất cả 11 giờ. Tính khoảng cách giữa hai bến A và B, biết vận tốc thực của ca nô là 22 km/h và vận tốc của dòng nước là 2 km/h
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 4 2023
Giải toán bằng cách lập phương trình:
Gọi vận tốc ca nô khi nước lặng là: \(x\) km/h ( \(x\) > 0)
Vận tốc ca nô khi xuôi dòng là: \(x\) + 5 ( km/h)
Thời gian ca nô xuôi dòng là: \(\dfrac{60}{x+5}\) (giờ)
Vận tốc ca nô khi ngược dòng là: \(x\) -5 ( km/h)
Thời gian ca nô ngược dòng là: \(\dfrac{60}{x-5}\) ( giờ)
Theo bài ra ta có phương trình:
\(\dfrac{60}{x+5}+\dfrac{60}{x-5}\) = 5 = \(\dfrac{60}{12}\)
⇒ \(\dfrac{1}{x+5}\) + \(\dfrac{1}{x-5}\) = \(\dfrac{1}{12}\)
⇒ 12 \(\times\) ( \(x+5+x-5\)) = (\(x\) + 5)(\(x-5\))
⇒ 12 \(\times\) 2\(x\) = \(x^2\) - 25
\(x^2\) - 25 - 24\(x\) = 0 ⇒ \(x^2\) - 24\(x\) - 25 = 0
ta có a - b + c = 1 - ( -24) - 25 = 0 ⇒ \(x\) = -1 ( loại); \(x\)= 25 ( thỏa mãn)
Vậy vận tốc ca nô khi nước lặng là 25 km/h
14 tháng 2 2021
Gọi vận tốc thực của ca nô là x (km/h)(x>0)Đổi: 11h30p = 11,5hVận tốc lúc xuôi dòng của ca nô là: x+6 (km/h)Vận tốc lúc ngược dòng của ca nô là: x-6 (km/h)Tổng thời gian cả đi lẫn về của ca nô là: 11,5 - 7 = 4,5 (giờ)Thời gian đi từ A xuôi dòng đến B là: 36/x+6 (giờ)Thời gian đi từ B ngược dòng về A là: 36/x-6 (giờ)Vì tổng thời gian cả đi lẫn về của ca nô là 4,5 (giờ) nên ta có phương trình:36/(x+6) + 36/(x-6) = 4,5<=> 36(x-6)/(x+6)(x-6) + 36(x+6)/(X+6)(x-6) = 4,5(x+6)(x-6)/(x+6)(x-6)=> 36x - 216 + 36x + 216 = 4,5x^2 - 162<=> 72x - 4,5x^2 + 162 = 0<=> 81(x + 2) - 4,5x(x + 2) = 0<=> (81 - 4,5x)(x + 2) = 0Vậy: 81 - 4,5x = 0 hoặc x + 2 = 0 <=> x = 18(nhận) <=> x = -2(loại) Suy ra vận tốc thực của ca nô là 18 (km/h)Vậy vận tốc của ca nô khi xuôi dòng là: x + 6 = 18 + 6 = 24 (km/h)
21 tháng 6 2023
Gọi vận tốc thật của cano là x
Thời gian đi là 36/(x+6)
Thời gian về là 36/(x-6)
Theo đề, ta có: 36/(x+6)+36/(x-6)=4,5
=>\(\dfrac{8}{x+6}+\dfrac{8}{x-6}=1\)
=>\(8x-48+8x+48=x^2-36\)
=>x^2-16x-36=0
=>(x-18)(x+2)=0
=>x=18
=>V xuôi dòg=18+6=24km/h
CM
8 tháng 10 2019
Gọi x (km/h) là vận tốc thực của ca nô. Điều kiện: x > 6
Vận tốc của ca nô khi xuôi dòng là x + 6 (km/h)
Vận tốc của ca nô khi ngược dòng là x – 6 (km/h)
Thời gian lúc ca nô đi xuôi dòng là 36/(x + 6) (giờ)
Thời gian lúc ca nô đi ngược dòng là 36/(x - 6) (giờ)
Thời gian ca nô đi và về:
11 giờ 30 phút – 7 giờ = 4 giờ 30 phút = 9/2 giờ
Theo đề bài, ta có phương trình:
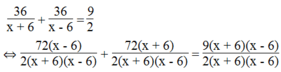
⇔ 72(x – 6) + 72(x + 6) = 9(x + 6)(x – 6)
⇔ 72x – 432 + 72x + 432 = 9x2 – 324
⇔ 9x2 – 144x – 324 = 0
⇔ x2 – 16x – 36 = 0
⇔ x2 + 2x – 18x – 36 = 0
⇔ x(x + 2) – 18(x + 2) = 0
⇔ (x + 2)(x – 18) = 0
⇔ x + 2 = 0 hoặc x – 18 = 0
x + 2 = 0 ⇔ x = -2 (loại)
x – 18 = 0 ⇔ x = 18 (thỏa)
Vậy vận tốc thực của ca nô là 18km/h, suy ra vận tốc của ca nô lúc xuôi dòng là 18 + 6 = 24 (km/h).
16 tháng 3 2020
gọi vận tốc của canô là x (x > 6)
vận tốc canô khi xuôi dòng là x + 6
vận tốc canô khi ngược dòng là x - 6
thời gian canô xuôi dòng: 36/(x + 6)
thời gian canô ngược dòng: 36/(x - 6)
thời gian cả đi và về là 4,5 giờ:
=> 36/(x + 6) + 36/(x - 6) = 4,5
4,5x^2 - 72x - 162 = 0
=> x= 18
=> vận tốc canô khi xuôi dòng là 24km/h
I
16 tháng 3 2020
Gọi Vận tốc xuôi dòng ca nô là \(x\) ( đk : \(x>6\))
VẬn tộc ngược dòng là :
\(x-6\)
Zận tốc xuôi dòng \(x+6\)
Thời gian đi từu A - B đi xuôi dòng nước là : \(\frac{36}{x+6}\)
Thời gian đi từ A - B đi ngược dòng nước là \(\frac{36}{x-6}\)
Thời gian ca nô đì từ A - B rồi quay từ B về A là
\(11h30-7h=4,5h\)
Theo bài ra ta có pt:
\(\frac{36}{x+6}+\frac{36}{x-6}=4,5=>x=18\)
D
27 tháng 3 2021
Thời gian đi từ A đến B là 11h30p-7h=3h30p
Đổi 3h30p=3,5h
Gọi thời gian xuôi dòng từ A đến B là: x(giờ)(ĐK x>0)
Thời gian từ B về A là: 3,5-x(giờ)
Vận tốc xuôi dòng là: (36/x)+6(km/h)
Vận tốc ngược dòng là: (36/3,5-x)-6(km/h)
Vì quãng đường AB ko đổi nên ta có phương trình
(36/x)+6-(36/3,5-x)-6=6
rồi giải tiếp nha !!
AH
Akai Haruma
Giáo viên
25 tháng 3 2021
Lời giải:
Tổng thời gian đi lẫn về là: $11h30-7=4h30=4,5$h
Gọi thời gian đi là $x$ (h) thì thời gian về là $4,5-x$ (h)
Vận tốc cano xuôi dòng: $\frac{AB}{x}=\frac{36}{x}$
Vận tốc cano ngược dòng: $\frac{AB}{4,5-x}=\frac{36}{4,5-x}$
Chênh lệch vận tốc xuôi dòng và ngược dòng bằng 2 lần vận tốc dòng nước, tức là:
$\frac{36}{x}-\frac{36}{4,5-x}=12$
$\Leftrightarrow \frac{3}{x}-\frac{3}{4,5-x}=1$
$\Rightarrow x^2-10,5x+13,5=0$
$\Rightarrow x=9$ hoặc $x=1,5$. Hiển nhiên $x< 4,5$ nên $x=1,5$
Vận tốc cano xuôi dòng là: $\frac{36}{1,5}=24$ (km/h)
KV
2 tháng 5 2022
Gọi \(x\) (km/h) là vận tốc thực của ca nô \(\left(x>6\right)\)
\(\Rightarrow\) Vận tốc lúc xuôi dòng là: \(x+6\) (km/h)
Thời gian đi xuôi dòng là: \(\dfrac{36}{x+6}\left(h\right)\)
Vận tốc lúc ngược dòng là: \(x-6\) (km/h)
Thời gian đi ngược dòng là: \(\dfrac{36}{x-6}\left(h\right)\)
Tổng thời gian ca nô đã đi: \(12h30'-8h=4h30'=\dfrac{9}{2}\left(h\right)\)
Theo đề bài, ta có phương trình: \(\dfrac{36}{x+6}+\dfrac{36}{x-6}=\dfrac{9}{2}\)
\(\Leftrightarrow36.2.\left(x-6\right)+36.2.\left(x+6\right)=9\left(x+6\right)\left(x-6\right)\)
\(\Leftrightarrow72x-432+72x+432=9x^2-324\)
\(\Leftrightarrow9x^2-144x-324=0\)
\(\Leftrightarrow x^2-16x-36=0\)
\(\Leftrightarrow x^2-18x+2x-36=0\)
\(\Leftrightarrow\left(x^2-18x\right)+\left(2x-36\right)=0\)
\(\Leftrightarrow x\left(x-18\right)+2\left(x-18\right)=0\)
\(\Leftrightarrow\left(x-18\right)\left(x+2\right)=0\)
\(\Leftrightarrow x-18=0;x+2=0\)
*) \(x-18=0\)
\(\Leftrightarrow x=18\) (nhận)
*) \(x+2=0\)
\(\Leftrightarrow x=-2\) (loại)
Vậy vận tốc ca nô lúc xuôi dòng là: 18 + 6 = 24 (km/h)
1 tháng 5 2022
Gọi vận tốc cano khi xuôi dòng là x + 6 ( x > 6 )
Vận tốc ngược dòng là x - 6
Tgian đi xuôi dòng là \(\dfrac{36}{x+6}\)
Tgian về ngược dòng là \(\dfrac{36}{x-6}\)
Tổng tgian từ lúc đi --> bến B
\(=12h30p-8h=4h30p=4,5h\)
Vì tổng tgian từ lúc đi --> bến B là 4,5h nên ta có pt
\(\dfrac{36}{x+6}+\dfrac{36}{x-6}=\dfrac{9}{2}\left(4,5h\right)\)
Giải pt trên ta đc\(\Rightarrow x=18+6=24km\)
Gọi khoảng cách giữu hai bến A và B là \(x\left(km;x>0\right)\)
Vận tốc khi ca nô xuôi dòng là : \(22+2=24\) km/h
Vận tốc khi ca nô ngược dòng là \(22-2=20\) km/h
Thời gian ca nô xuôi dòng là : \(\dfrac{x}{24}\left(h\right)\)
Thời gian ca nô ngược dòng là \(\dfrac{x}{20}\left(h\right)\)
Vì cả đi lẫn về hết 11 giờ nên ta có phương trình :
\(\dfrac{x}{24}+\dfrac{x}{20}=11\)
\(\Leftrightarrow5x+6x=1320\)
\(\Leftrightarrow11x=1320\)
\(\Leftrightarrow x=120\left(nhận\right)\)
Vậy khoảng cách giữa hai bến A và B là \(120km\)
gọi AB là x
quãng đường đi từ A đến B là x chia 24
quãng đường về từ A đến B là x chia 20
ta có pt
x : 24 + x : 20 = 11
5x + 6x = 1320
11x = 1320
x=120 ( km )
vậy quãng đường AB dài 120 km