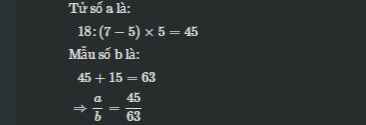Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1: B là số nguyên
=>n-3 thuộc {1;-1;5;-5}
=>n thuộc {4;2;8;-2}
3:
a: -72/90=-4/5
b: 25*11/22*35
\(=\dfrac{25}{35}\cdot\dfrac{11}{22}=\dfrac{5}{7}\cdot\dfrac{1}{2}=\dfrac{5}{14}\)
c: \(\dfrac{6\cdot9-2\cdot17}{63\cdot3-119}=\dfrac{54-34}{189-119}=\dfrac{20}{70}=\dfrac{2}{7}\)
Ta có: a/b=16/23
=>a/16=b/23
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
a/16=b/23=b-a/23-16=21/7=3
=>a=16.3=48
=>b=23.3=69
Vậy a=48,b=69
Gọi X là số lần chúng ta đã rút gọn tử số và mẫu số của phân số a/b, ta có phương trình:
23X-16X=21 -> 7X= 21 -> X=3;
Vậy phân số a/b =48/69
Hiệu số phần bằng nhau là:
23 - 16 = 7
Tử a là:
21 : 7 x 16 = 48
Mẫu b là:
48 + 21 = 69
Vậy phân số cần tìm là 48/69=16/23
a) Ta có: \(A=\dfrac{1+3+5+...+19}{21+23+25+...+39}\)
\(=\dfrac{\left(1+19\right)+\left(3+17\right)+...+\left(9+11\right)}{\left(21+39\right)+\left(23+37\right)+...+\left(29+31\right)}\)
\(=\dfrac{20\cdot5}{60\cdot5}=\dfrac{1}{3}\)
