Giúp mình câu c bài 26 với🙏🙏🙏🙏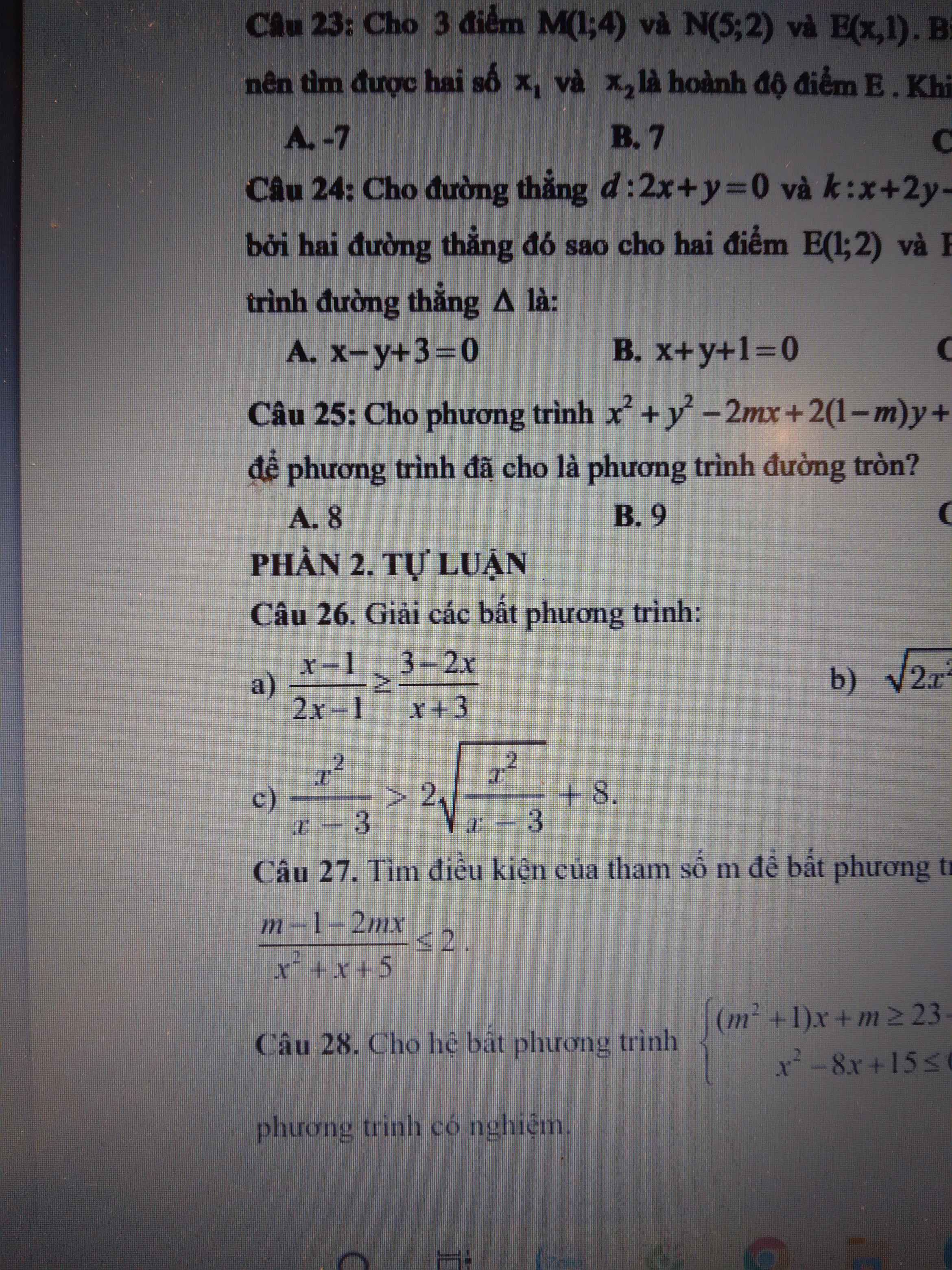
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
1
1 tháng 7 2023
15:
b: Gọi I(a;b)
Theo đề, ta có: d(I;d)=d(I;d')=căn 5
=>3a-b+3=căn 5*căn 10=5*căn 2 và a-3b+9=5căn 2
=>|3a-b+3|=|a-3b+9|
=>2a+2b=6 và 2a-4b=12
=>a=1 và b=2
=>I(1;2)
Phương trình (C) là:
(x-1)^2+(y-2)^2=5
c: (C): x^2+y^2+4x-y+4=0
=>(x+2)^2+(y-1/2)^2=1/4
=>I(-2;1/2);R=1/2
=>I'(2;1/2)
Phương trình (C') là:
(x-2)^2+(y-1/2)^2=1/4
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
a.
Đường tròn có tâm \(\left\{{}\begin{matrix}x_I=2m\\y_I=-m-3\end{matrix}\right.\)
\(\Rightarrow x_I+2y_I=2m+2\left(-m-3\right)=-6\)
\(\Leftrightarrow x_I+2y_I+6=0\)
Hay quỹ tích tâm I của đường tròn là đường thẳng có pt: \(x+2y+6=0\)
b.
Gọi H là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}AH=\dfrac{1}{2}AB=3\\IH\perp AB\end{matrix}\right.\) \(\Rightarrow IH=d\left(I;d\right)\)
\(R=IA=\sqrt{\left(2m\right)^2+\left(-m-3\right)^2-\left(5m^2-6m-16\right)}=5\)
\(\Rightarrow IH=\sqrt{IA^2-AH^2}=4\)
\(d\left(I;d\right)=\dfrac{\left|3.2m-4\left(-m-3\right)+12\right|}{\sqrt{3^2+\left(-4\right)^2}}=4\)
\(\Leftrightarrow\left|10m+24\right|=20\Rightarrow\left[{}\begin{matrix}m=-\dfrac{2}{5}\\m=-\dfrac{22}{5}\end{matrix}\right.\)
1 tháng 9 2021
\(\dfrac{1}{\sqrt{\dfrac{5}{7}}+\sqrt{\dfrac{5}{13}}+1}+\dfrac{1}{\sqrt{\dfrac{7}{13}}+\sqrt{\dfrac{7}{5}}+1}+\dfrac{1}{\sqrt{1\dfrac{6}{7}}+\sqrt{2\dfrac{3}{5}}+1}\\ =\dfrac{1}{\dfrac{\sqrt{5}}{\sqrt{7}}+\dfrac{\sqrt{5}}{\sqrt{13}}+\dfrac{\sqrt{5}}{\sqrt{5}}}+\dfrac{1}{\dfrac{\sqrt{7}}{\sqrt{13}}+\dfrac{\sqrt{7}}{\sqrt{5}}+\dfrac{\sqrt{7}}{\sqrt{7}}}+\dfrac{1}{\dfrac{\sqrt{13}}{\sqrt{7}}+\dfrac{\sqrt{13}}{\sqrt{5}}+\dfrac{\sqrt{13}}{\sqrt{13}}}\\ =\left(\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{7}}+\dfrac{1}{\sqrt{13}}\right)\cdot\dfrac{1}{\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{7}}+\dfrac{1}{\sqrt{13}}}\\ =1\)
giải giúp mình bài 3 với nhé 🙏🙏🙏
4 tháng 12 2021
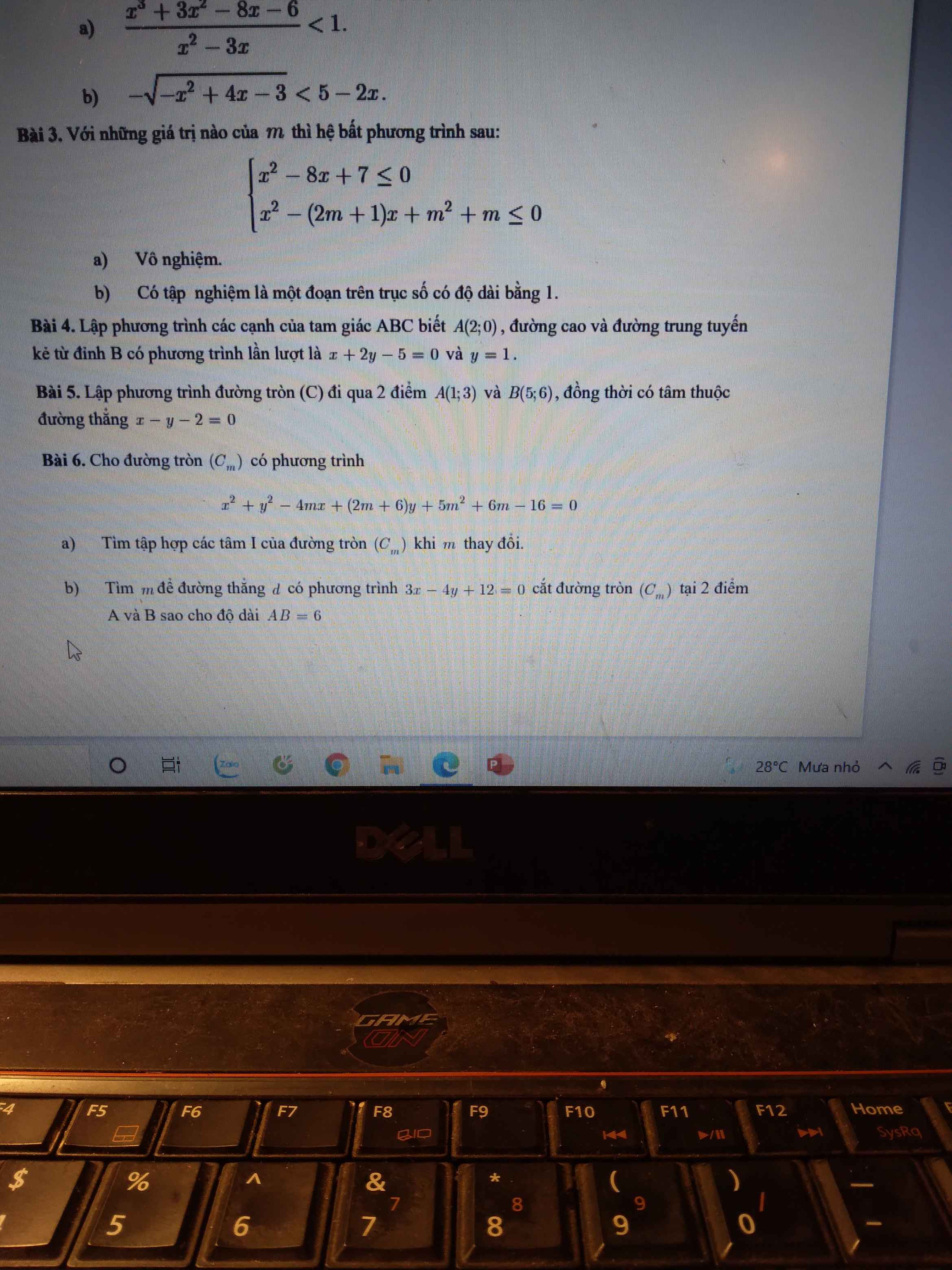
Bài 3:
Gọi 4 số chẵn lt là \(a,a+2,a+4,a+6\left(a\in N\right)\)
Ta có \(\dfrac{a+a+2+a+4+a+6}{4}=2007\)
\(\Rightarrow a\times4+12=2007\times4=8028\\ \Rightarrow a\times4=8016\\ \Rightarrow a=2004\)
Vậy 4 số cần tìm là 2004,2006,2008,2010
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2022
4b.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow cosa< 0\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{3}{4}\)
\(tan\left(a+\dfrac{\pi}{3}\right)=\dfrac{tana+tan\left(\dfrac{\pi}{3}\right)}{1-tana.tan\left(\dfrac{\pi}{3}\right)}=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\left(-\dfrac{3}{4}\right).\sqrt{3}}=...\)
c.
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{5}{13}\)
\(cos\left(\dfrac{\pi}{3}-a\right)=cos\left(\dfrac{\pi}{3}\right).cosa+sin\left(\dfrac{\pi}{3}\right).sina=\dfrac{1}{2}.\dfrac{5}{13}+\left(-\dfrac{12}{13}\right).\dfrac{\sqrt{3}}{2}=...\)
Đặt \(\sqrt{\dfrac{x^2}{x-3}}=a\left(a>=0\right)\)
Theo đề, ta có bất phương trình:
\(a^2>2a+8\)
=>(a-4)(a+2)>0
=>a-4>0
\(\Leftrightarrow\dfrac{x^2}{x-3}>16\)
\(\Leftrightarrow x^2-16x+48>0\)
\(\Leftrightarrow x\in R\)
Vậy: S=R\{3}