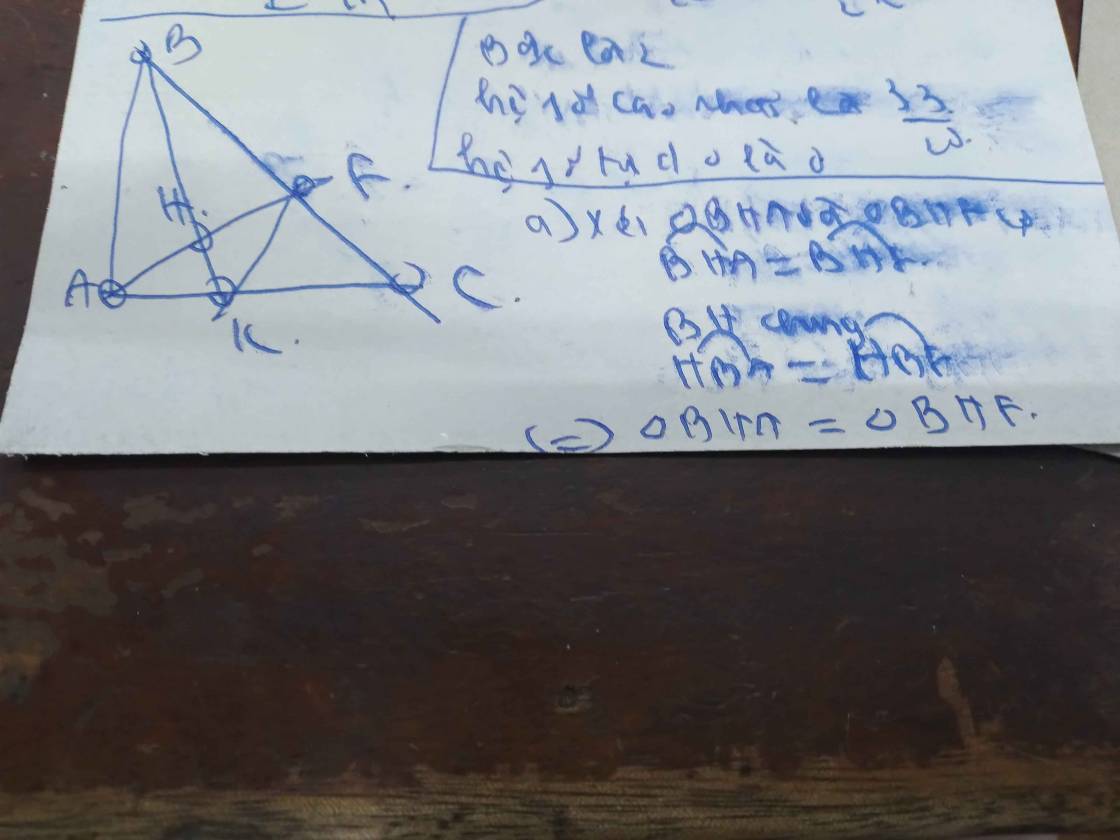
cho tam giác ABC vuông tại A, kẻ phân giác BK của góc B (K thuộc AC ), kẻ AE vuông góc với BK tại H và E thuộc BC
a. vẽ hình
b. chứng minh : tam giác BHA = tam giác BHE
c. chứng minh : EK vuông góc BC
d. chứng minh : AK < KC
giúp mình với ạ ,tối mình nộp rồi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 3 2023
a: Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
góc HBA=góc HBE
=>ΔBHA=ΔBHE
b: Xét ΔBAK và ΔBEK có
BA=BE
góc ABK=góc EBK
BK chung
=>ΔBAK=ΔBEK
=>góc BEK=90 độ
=>KE vuông góc BC
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
10 tháng 5 2022
a/
Xét tg BAE và tg BKE có
BE chung; BA=BK (gt)
\(\widehat{ABE}=\widehat{KBE}\left(gt\right)\)
=> tg BAE = tg BKE (c.g.c)
b/
Ta có tg BAE = tg BKE (cmt) => AE=KE và \(\widehat{BAE}=\widehat{BKE}=90^o\)
\(\Rightarrow EK\perp BC\)
c/
Xét tg vuông CKE có EC là cạnh huyền => KE<EC (trong tg vuông cạnh huyền là cạnh có độ dài lớn nhất)
Mà AE=KE (cmt)
=> AE<EC
d/ Gọi D là giao của BE với AK
Xét tg ABK có
BA=BK => tg ABK cân tại B
BD là phân giác \(\widehat{ABK}\)
=> BD là trung tuyến của tg ABK (trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường trung tuyến)
Có AI là trung tuyến của tg ABK
=> G là trong tâm của tg ABK => BG=2.DG
Xét tg DKG có
\(DK=DA=\dfrac{AK}{2}\) (BD là trung tuyến)
Ta có
\(DG+DK>KG\) (trong tg tổng độ dài 2 cạnh lớn hơn độ dài cạnh còn lại)
\(\Rightarrow DG+\dfrac{AK}{2}>KG\) Mà \(BG=2.DG\Rightarrow BG>DG\Rightarrow BG+\dfrac{AK}{2}>KG\)
31 tháng 3 2021
a) Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
\(\widehat{ABH}=\widehat{EBH}\)(BH là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔBHA=ΔBHE(cạnh góc vuông-góc nhọn kề)
31 tháng 3 2021
b) Ta có: ΔBHA=ΔBHE(cmt)
nên BA=BE(hai cạnh tương ứng)
Xét ΔBAD và ΔBED có
BA=BE(cmt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔBAD=ΔBED(c-g-c)
Suy ra: \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
hay DE\(\perp\)BC(đpcm)
18 tháng 3 2021
a) Sửa đề: Trên HC lấy E sao cho HE=HB và c/m ΔBHA=ΔEHA
Xét ΔBHA vuông tại H và ΔEHA vuông tại H có
AH chung
BH=EH(gt)
Do đó: ΔBHA=ΔEHA(hai cạnh góc vuông)
