Cho tam giác ABC vuông ở A, đường cao AH chia cạnh huyền BC thành 2 đoạn ; BH,CH có độ dài lần lượt là 4cm và 9cm . Gọi D và E lần lượt là hình chiếu của điểm H trên AB và AC .Tính a, DE
b, Cắt đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M và N . chứng minh M là trung điểm của BH, N là trung điểm của CH.
c, Tính diện tích tứ giác DEMN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 11 2021
a: \(AH=2\sqrt{6}\left(cm\right)\)
\(AB=2\sqrt{10}\left(cm\right)\)
\(AC=2\sqrt{15}\left(cm\right)\)
15 tháng 10 2021
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2\sqrt{6}\left(cm\right)\\AC=2\sqrt{15}\left(cm\right)\\AB=2\sqrt{10}\left(cm\right)\end{matrix}\right.\)
CM
13 tháng 10 2018
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A
Ta có: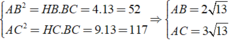
Vậy S A B C = 1 2 A B . A C = 1 2 . 2 13 . 3 13 = 39 c m 2
Chọn đáp án A.
10 tháng 10 2021
Ta có : HB + HC = BC = 8 cm
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AB^2=BH.BC=2.8\Rightarrow AB=4cm\)
* Áp dụng hệ thức : \(AC^2=CH.BC=6.8\Rightarrow AC=4\sqrt{3}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{16\sqrt{3}}{8}=2\sqrt{3}cm\)
15 tháng 3 2019
Không mất tính tổng quát
g/s: BH=9m , CH=16m
Ta có: BC=BH+HC=25m
Xét tam giác ABC vuông tại A
=> \(AB^2+AC^2=BC^2=625\)
Xét tam giác ABH và ACH vuông tại H có: \(AB^2=AH^2+BH^2=AC^2-CH^2+BH^2\)=> \(AB^2=AC^2-16^2+9^2=AC^2-175\)
=> \(AC^2-175+AC^2=625\Rightarrow AC^2=400\Rightarrow AC=20\)m
=> \(AB^2=AC^2-175=225\Rightarrow AC=15\)m
Chu vi= 15+20+25=60 m
27 tháng 7 2017
B1: Gọi Tam giác ABC vuông tại A có AH là đ/cao chia cạnh huyền thành 2 đoạn HB và HC
AH2=HB x HC =3x4=12
AH=căn 12 r tính mấy cạnh kia đi
B2: Ta có AB/3=AC/4 suy ra AB = 3AC/4
Thế vào cong thức Pytago Tam giác ABC tính máy cái kia
6 tháng 4 2023
Xét ΔACB vuông tại A có AH là đường cao
nên AH^2=HB*HC
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
=>AC=20(cm)
