Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc vs (ABCD), SB=SD= a căn 5 , gọi M là trung điên của SD. Tính góc giữa 2 mp (AMC) và (ABCD). Nếu đc thì vẽ giùm mình cái hình luôn ạ. Cảm ơn rất nhiều...
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 7 2023
1: AC=căn a^2+a^2=a*căn 2
=>SC=căn SA^2+AC^2=a*căn 8
SB=căn AB^2+SA^2=a*căn 7
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
=>SB vuông góc BC
CM
7 tháng 2 2017
Đáp án là D
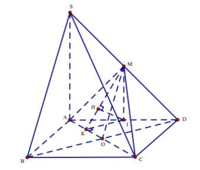
+ Gọi O là giao điểm của AC,BD
⇒ MO \\ SB ⇒ SB \\ ACM
⇒ d SB,ACM = d B,ACM = d D,ACM .
+ Gọi I là trung điểm của AD ,
M I \ \ S A ⇒ M I ⊥ A B C D d D , A C M = 2 d I , A C M .
+ Trong ABCD: IK ⊥ AC (với K ∈ AC ).
+ Trong MIK: IH ⊥ MK (với H ∈ MK ) (1) .
+ Ta có: AC ⊥ MI ,AC ⊥ IK ⇒ AC ⊥ MIK
⇒ AC ⊥ IH (2) .
Từ 1 và 2 suy ra
IH ⊥ ACM ⇒ d I ,ACM = IH .
+ Tính IH ?
- Trong tam giác vuông MIK. : I H = I M . I K I M 2 + I K 2 .
- Mặt khác: M I = S A 2 = a , I K = O D 2 = B D 4 = a 2 4
⇒ I H = a a 2 4 a 2 + a 2 8 = a 3
Vậy d S B , A C M = 2 a 3 .
Lời giải khác
CM
18 tháng 3 2019
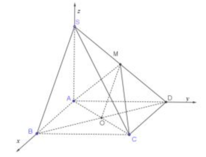
Đáp án B
Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A
Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C
Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3
⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2021
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\) (1)
Tam giác SAB vuông cân tại A (do SA=SB=a)
\(\Rightarrow AM\perp SB\) (trung tuyến đồng thời là đường cao) (2)
(1);(2)\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\)
\(\Rightarrow SC\perp\left(AMN\right)\Rightarrow\left(SAC\right)\perp\left(AMN\right)\)
Từ A kẻ \(AH\perp SC\Rightarrow H\in\left(AMN\right)\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{HAC}\) là góc giữa (AMN) và (ABCD)
\(AC=a\sqrt{2}\) ; \(SC=a\sqrt{3}\)
\(sin\widehat{HAC}=cos\widehat{SCA}=\dfrac{AC}{SC}=\sqrt{\dfrac{2}{3}}\Rightarrow\widehat{HAC}\approx54^044'\)
M là trung điểm của SD
Gọi O là tâm đáy \(\Rightarrow OD\perp AC\) (đường chéo hình vuông)
Gọi N là trung điểm AD \(\Rightarrow\) MN là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}SA=\dfrac{a\sqrt{5}}{2}\\MN||SA\end{matrix}\right.\)
Do \(SA\perp\left(ABCD\right)\Rightarrow MN\perp\left(ABCD\right)\Rightarrow MN\perp AC\)
Gọi P là trung điểm AO \(\Rightarrow\) NP là đường trung bình tam giác OAD
\(\Rightarrow\left\{{}\begin{matrix}NP=\dfrac{1}{2}OD=\dfrac{a\sqrt[]{2}}{4}\\NP||OD\end{matrix}\right.\)
Mà \(OD\perp AC\Rightarrow NP\perp AC\)
\(\Rightarrow AC\perp\left(MNP\right)\)
Lại có AC là giao tuyến (AMC) và (ABCD)
\(\Rightarrow\widehat{MPN}\) là góc giữa (AMC) và (ABCD)
\(tan\widehat{MPN}=\dfrac{MN}{NP}=\sqrt{10}\Rightarrow\widehat{MPN}\approx72^027'\)