Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a, BC = a√3 và SA vuông góc (ABCD). Góc giữa SC và mặt phẳng (ABCD) bằng 45°. Gọi M là trung điểm của đoạn OA. Chứng minh (SAC) vuông góc (SBM)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 6 2019
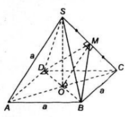
a) Theo giả thiết, S.ABCD là hình chóp đều và đáy ABCD là hình vuông nên SO ⊥ (ABCD) ( tính chất hình chóp đều)
Đáy ABCD là hình vuông cạnh a nên
=> Góc giữa hai mặt phẳng (MBD) và (ABCD) là 45 o
CM
15 tháng 6 2018
Đáp án B
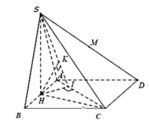
Dễ thấy: S C H ^ = 45 ∘ Gọi H là trung điểm của AB ta có S H ⊥ A B ⇒ S H ⊥ A B C D .
Ta có: S H = H C = a 17 2 .
Ta có: d = d M , S A C = 1 2 d D , S A C
Mà 1 2 d D , S A C = 1 2 d B , S A C nên d = d H , S A C
Kẻ H I ⊥ A C , H K ⊥ S I ⇒ d H , S A C = H K
Ta có: H I = A B . A D 2 A C = a 5 5
Từ đó suy ra: d = H K = S H . H I S I = a 1513 89 .
15 tháng 6 2023
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 3 2021
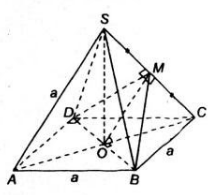
Gọi N là trung điểm AB \(\Rightarrow MN\perp AD\Rightarrow AD\perp\left(SMN\right)\Rightarrow AD\perp SM\)
Mặt khác: \(MN=AB=a\) ; \(SM=SN=\sqrt{SO^2+\left(\dfrac{MN}{2}\right)^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow SM^2+SN^2=MN^2\Rightarrow\Delta SMN\) vuông cân tại S hay \(SM\perp SN\)
\(\Rightarrow SM\perp\left(SAD\right)\)
Trong mp (SBC), dựng hình chữ nhật SMCP \(\Rightarrow CP||SM\Rightarrow CP\perp\left(SAD\right)\)
\(\Rightarrow\) SP là hình chiếu vuông góc của SC lên (SAD) hay \(\widehat{CSP}=\phi\)
\(AC=a\sqrt{5}\Rightarrow SC=\sqrt{SO^2+\left(\dfrac{AC}{2}\right)^2}=\dfrac{a\sqrt{6}}{2}\); \(SP=MC=\dfrac{BC}{2}=a\)
\(\Rightarrow CP=\sqrt{SC^2-SP^2}=\dfrac{a\sqrt{2}}{2}\)
\(sin\phi=\dfrac{CP}{SC}=\dfrac{\sqrt{3}}{3}\)
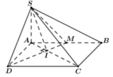
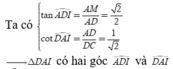
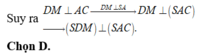
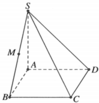
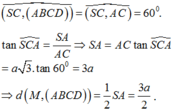
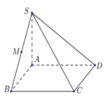
\(AC=\sqrt{AB^2+BC^2}=2a\) \(\Rightarrow AO=\dfrac{1}{2}AC=a\) ; \(AM=\dfrac{1}{2}AO=\dfrac{a}{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD) \(\Rightarrow\widehat{SCA}=45^0\)
\(\Rightarrow SA=AC.tan45^0=2a\)
\(AB^2=a^2\) ; \(AM.AC=\dfrac{a}{2}.2a=a^2\Rightarrow AB^2=AM.AC\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AC}{AB}\Rightarrow\Delta ABM\sim\Delta ACB\left(c.g.c\right)\)
\(\Rightarrow\widehat{AMB}=\widehat{ABC}=90^0\Rightarrow BM\perp AC\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BM\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\left(SBM\right)\perp\left(SAC\right)\)