Question

[Nguyễn Mai Nhan Ngọc]

Cho tam giác ABC có Â = 60 độ. Các tia phân giác của góc B và C cắt nhau tại I, lần lượt cắt AC và AB tại D và E. Phân giác góc BIC cắt BC tại F

a) Tính số đo góc BIC

b) Chứng minh: ID=IE=IF

c) Chứng minh: Tam giác EDF là tam giác đều

d) Chứng minh: I là giao điểm của cả hai đường phân giác của hai tam giác ABC và DEF

Answer 1

[Nguyễn Đức Anh]

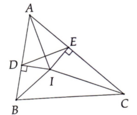
a, 

ta có 

A + B+ C = \(180^0\)

B + C  = \(180^0\)-  A

mà BI là phân giác góc B

IBC = \(\frac{1}{2}\)B

CI là phân giác góc C 

ICB = \(\frac{1}{2}\)C

suy ra 

IBC + ICB = \(\frac{1}{2}\)B + \(\frac{1}{2}\)C = \(\frac{1}{2}\)( B + C ) = \(\frac{1}{2}\)( \(180^0\)- A ) = \(\frac{1}{2}\) \(\left(180^0-60^0\right)\)= \(60^0\)

mà IBC + ICB + BIC = \(180^0\)

suy ra BIC = \(180^0\)- ( IBC + ICB )

          BIC = \(180^0\)- \(60^0\) 

          BIC = \(120^0\)

b,

ta có vì I là giao điểm của phân giác góc B và C 

suy ra phân giác góc A đi qua I suy ra tia AI trùng tia IF suy ra AF là phần giác góc A mà I cách đều AB ; AC ; BC 

nên IE = ID = IF

c,

ta có EIB + BIC =\(180^0\) 

       EIB = \(180^0-120^0\)

     EIB = \(60^0\)

    Mà EIB đối đỉnh góc DIC 

suy ra DIC = EIB =  \(60^0\)

vì IF là tia phân giác góc BIC 

nên BIF = CIF = \(\frac{1}{2}\)\(120^0\)= \(60^0\)

EIF = BIE + BIF = \(60^0+60^0=120^0\)

DIF = DIC + CIF =  \(60^0+60^0=120^0\)

xét tam giác EIF và DIF có 

EIF = DIF = \(120^0\)

IF là cạnh chung 

IE = ID 

suy ra tam giác EIF = tam giác DIF ( c-g-c )

suy ra EF = DF 

ta có góc BIC đối đỉnh góc EID 

nên BIC = EID = \(120^0\)

xét tam giác EIF và EID có 

EID = EIF =\(120^0\)

ID = IF 

IE cạnh chung 

suy ra tam giác DIE = tam giác FIE ( c-g-c )

suy ra ED = EF 

mà EF = DF 

suy ra ED = EF = DF

suy ra tam giác EDF là tam giác đều 

d,

ta có IE = IF = ID 

nên I cách đều 3 đỉnh tam giác DFE nên I là giao điểm của 3 đường trung trực tam giác DEF 

mà trong tam giác đều 3 đường trung trực đồng thời là 3 đường phân giác của tam giác đó 

suy ra I là giao điểm của hai đường phân giác trong tam giác ABC vá DEF