Tìm m để phương trình \(\dfrac{2}{x-m}-\dfrac{5}{x+m}=1\)( x là ẩn số ) có 1 nghiệm bằng 3. Tổng các giá trị m tìm được bằng :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(đk:\left\{{}\begin{matrix}\Delta\ge0\\0< x1\le x2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5^2-4\left(-m^2+m+6\right)\ge0\\\left\{{}\begin{matrix}x1+x2>0\\x1x2>0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4m^2-4m+1=\left(2m-1\right)^2\ge0\left(đúng\right)\\\left\{{}\begin{matrix}5>0đúng\\-m^2+m+6>0\Leftrightarrow-2< m< 3\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow-2< m< 3\)
\(\Rightarrow\dfrac{1}{\sqrt{x1}}+\dfrac{1}{\sqrt{x2}}=\dfrac{3}{2}\Leftrightarrow\dfrac{\sqrt{x1}+\sqrt{x2}}{\sqrt{x1x2}}=\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{x1+x2+2\sqrt{x1x2}}{x1x2}=\dfrac{9}{4}\Leftrightarrow\dfrac{5+2\sqrt{-m^2+m+6}}{-m^2+m+6}=\dfrac{9}{4}\)
\(đặt::\sqrt{-m^2+m+6}=t\ge0\Rightarrow\dfrac{5+2t}{t^2}=\dfrac{9}{4}\)
\(\Rightarrow9t^2-8t-20=0\Leftrightarrow\left[{}\begin{matrix}t=2\\t=-\dfrac{10}{9}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{-m^2+m+6}=2\Leftrightarrow\left[{}\begin{matrix}m=2\left(tm\right)\\m=-1\left(tm\right)\end{matrix}\right.\)

với m> -4 thì đa thức co nghiệm là số hữu tỷ, không lẽ bn học trg chuyên mà không hiểu?

a) Ta xét :
\(\Delta'=\left(m-2\right)^2+2m=m^2-2m+4=\left(m-1\right)^2+3\ge3>0\)
Vì \(\Delta'>0\)nên phương trình trên luôn có hai nghiệm phân biệt.
b) Dễ thấy : x1<x2 nên ta có :
\(x_1=\frac{2\left(m-2\right)-\sqrt{\left(m-1\right)^2+3}}{2}=m-2-\sqrt{\left(m-1\right)^2+3}\) ; \(x_2=\frac{2\left(m-2\right)+\sqrt{\left(m-1\right)^2+3}}{2}=m-2+\sqrt{\left(m-1\right)^2+3}\)
\(x_2-x_1=x_1^2\Leftrightarrow2\sqrt{\left(m-1\right)^2+3}=\left(m-2-\sqrt{\left(m-1\right)^2+3}\right)^2\)
\(\Leftrightarrow\left(m-2\right)^2+\left(m-1\right)^2+3-2\left(m-2\right)\sqrt{\left(m-1\right)^2+3}=2\sqrt{\left(m-1\right)^2+3}\)
\(\Leftrightarrow m=2\)
Vậy m = 2






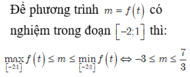

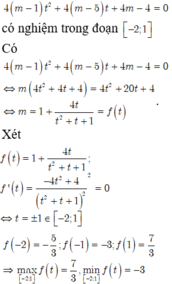
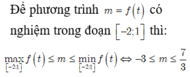
Thay x=3 vào pt ta có:
\(\dfrac{2}{x-m}-\dfrac{5}{x+m}=1\\ \Leftrightarrow\dfrac{2}{3-m}-\dfrac{5}{3+m}=1\\ \Leftrightarrow\dfrac{2\left(3+m\right)-5\left(3-m\right)}{\left(3-m\right)\left(3+m\right)}=1\\ \Rightarrow6+2m-15+5m=3^2-m^2\\ \Leftrightarrow-9+7m-9+m^2-0\\ \Leftrightarrow m^2+7m-18=0\\ \Leftrightarrow\left[{}\begin{matrix}m=2\\m=-9\end{matrix}\right.\)