Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Xét tứ giác BCEF có
^CEB = ^CFB = 900
mà 2 góc này kề, cùng nhìn cạnh BC
Vậy tứ giác BCEF là tứ giác nt 1 đường tròn
b, Xét tứ giác AEHF có
^HEA = ^HFA = 900
Vậy tứ giác AEHF là tứ giác nt 1 đường tròn
c, Ta có ^AMN = ^ACN ( góc nt chắn cung AN )
^ANM = ^MBA ( góc nt chắn cung MA )
mà ^ACN = ^MBA ( tứ giác BCEF nt và 2 góc cùng nhìn cung CF )
=> ^AMN = ^ANM Vậy tam giác AMN cân tại A
=> AN = AM
d, Ta có : ^CBM = ^CFE ( góc nt chắn cung CE của tứ giác BCEF )
mặt khác : ^CNM = ^CBM ( góc nt chắn cung CM )
=> ^CFE = ^CNM, mà 2 góc này ở vị trí đồng vị )
=> MN // EF
e, Ta có AO là đường cao tam giác MAN
mà MN // EF ; AO vuông MN => AO vuông EF
xét tứ giác BFHD có
góc BFH + góc BDH = 180
mà nó là 2 góc đối => nội tiếp => góc FDH = góc FBE
chứng minh tương tự với tứ giác CEHD
=> góc HDE = góc HCE
Xét tứ giác BFEC có
góc BFC = góc BEF = 90
mà nó là 2 góc kề => tứ giác nội tiếp
mà góc BEC = 1/2 sđ BC = 90 => SĐ BC = 180 => BC là đường kính mà I là trung điểm BC => I là tâm đường tròn ngoại tiếp tứ giác BFEC
=> góc FIE = góc FBE + góc FCE
=> Góc FIE = góc FDH+góc HDE => góc FIE = góc FDE
mà nó là 2 góc kề => nội tiếp
=> điều phải cm
b) Xét tứ giác BFEC có:
∠(BFC) = 90 0 (Do CF là đường cao)
∠(BEC ) = 90 0 (Do BE là đường cao)
⇒ E và F cùng nhìn BC dưới một góc bằng nhau
⇒ Tứ giác BFEC nội tiếp được đường tròn
⇒ Bốn điểm B, E, F, C cùng nằm trên đường tròn
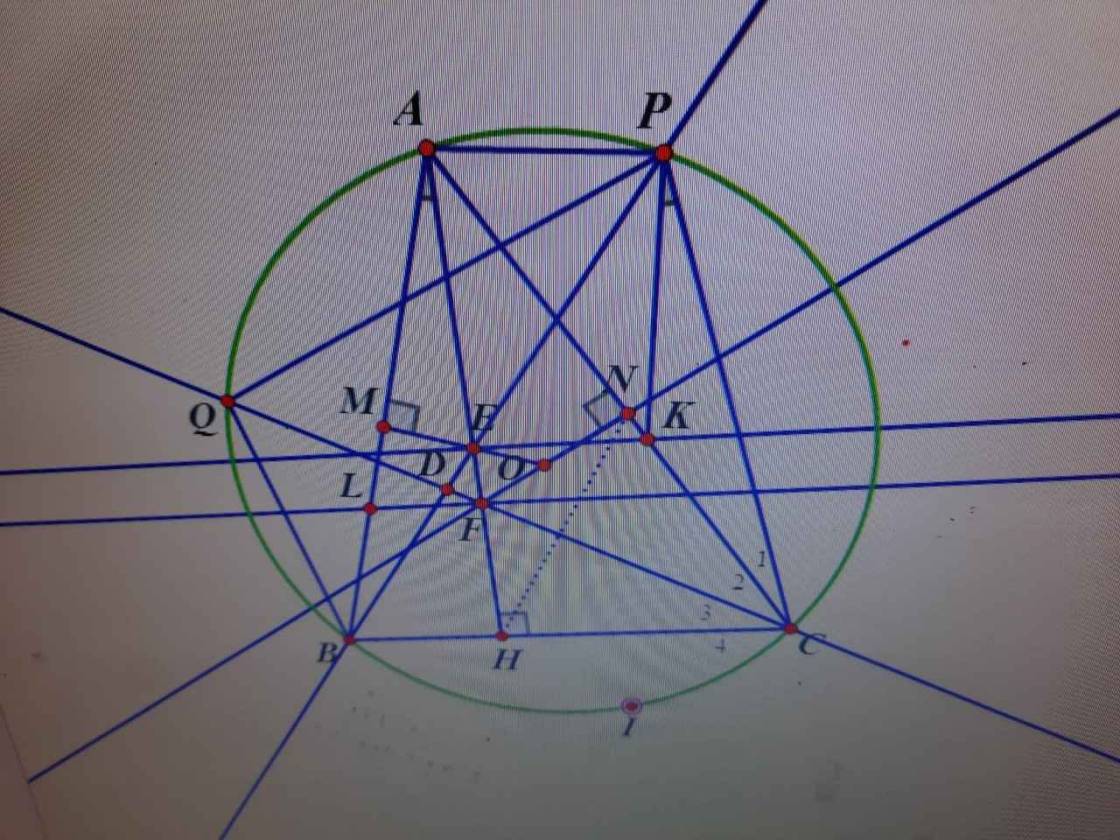
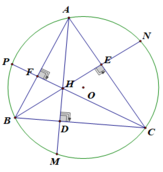
a: Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó:BCEF là tứ giác nội tiếp
b: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=180^0\)
Do đó: AEHF là tứ giác nội tiếp
giúp mình câu c,d,e đi