Tam giác cân ABC cos BC√5=AB√2=AC√2. Góc giữa hai đường thẳng chứa trung tuyến BM và CN bằng bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 4 2021
a) Sửa đề: Cm AG vuông góc với BC
Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)
\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AN=NB=AM=MC
Xét ΔNBC và ΔMCB có
NB=MC(cmt)
\(\widehat{NBC}=\widehat{MCB}\)(hai góc ở đáy của ΔABC cân tại A)
BC chung
Do đó: ΔNBC=ΔMCB(c-g-c)
Suy ra: \(\widehat{NCB}=\widehat{MBC}\)(hai góc tương ứng)
hay \(\widehat{GBC}=\widehat{GCB}\)
Xét ΔGBC có \(\widehat{GBC}=\widehat{GCB}\)(cmt)
nên ΔGBC cân tại G(Định lí đảo của tam giác cân)
Suy ra: GB=GC(hai cạnh bên)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: GB=GC(cmt)
nên G nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AG là đường trung trực của BC
hay AG\(\perp\)BC(đpcm)
GH
19 tháng 6 2023
a)
Có 2 trung tuyến BN, CM cắt nhau suy ra \(BN\perp AM\)
Gọi G là trọng tâm tam giác ABC, ta có \(BG=\dfrac{2}{3}BN=\dfrac{2}{3}.4=\dfrac{8}{3}\left(cm\right)\)
Trong tam giác ABN vuông tại A, đường cao AG, ta có:
\(AB^2=BG.BN\) (hệ thức lượng)
\(\Rightarrow AB=\sqrt{\dfrac{8}{3}.4}=\dfrac{4\sqrt{6}}{3}\left(cm\right)\)
Tam giác ABN vuông tại A
\(\Rightarrow AN^2=BN^2-AB^2\\ \Rightarrow AN=\sqrt{4^2-\left(\dfrac{4\sqrt{6}}{3}\right)^2}=\dfrac{4\sqrt{3}}{3}\left(cm\right)\)
Mà N là trung điểm AC => AC = \(\dfrac{8\sqrt{3}}{3}\left(cm\right)\)
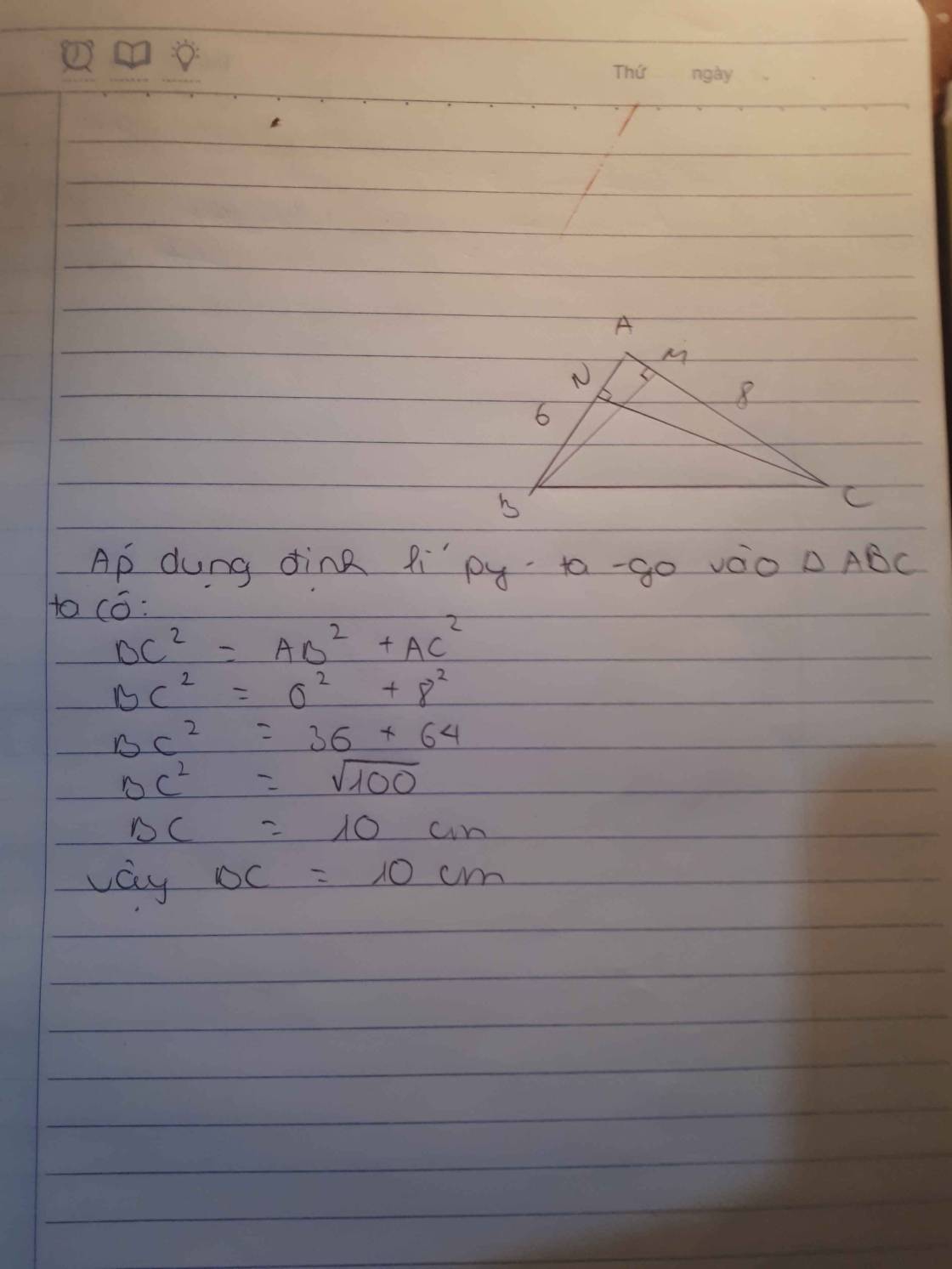
Áp dụng đl pytago vào tam giác ABC:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{4\sqrt{6}}{3}\right)^2+\left(\dfrac{8\sqrt{3}}{3}\right)^2}=4\sqrt{2}\left(cm\right)\)
Thừa dữ kiện AM = 3cm, bạn coi kỹ đề đủ/ đúng hết chưa thì cmt để chút mình coi lại bài giải
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2023
Gọi G là trọng tâm tam giác \(\Rightarrow\) tọa độ G là nghiệm:
\(\left\{{}\begin{matrix}x+7y-10=0\\x-2y+2=0\end{matrix}\right.\) \(\Rightarrow G\left(\dfrac{2}{3};\dfrac{4}{3}\right)\)
Gọi D là trung điểm BC, theo tính chất trọng tâm:
\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}\Rightarrow\left\{{}\begin{matrix}\dfrac{2}{3}\left(x_D-1\right)=-\dfrac{1}{3}\\\dfrac{2}{3}\left(y_D-3\right)=-\dfrac{5}{3}\\\end{matrix}\right.\) \(\Rightarrow D\left(\dfrac{1}{2};\dfrac{1}{2}\right)\)
Do B thuộc BM nên tọa độ có dạng: \(B\left(10-7b;b\right)\)
Do D là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}x_C=2x_D-x_B=7b-9\\y_C=2y_D-y_B=1-b\end{matrix}\right.\) \(\Rightarrow C\left(7b-9;1-b\right)\)
Do C thuộc CN nên:
\(7b-9-2\left(1-b\right)+2=0\Rightarrow b=1\)
\(\Rightarrow B\left(3;1\right)\)
Biết tọa độ 2 điểm B; D thuộc BC, bây giờ có thể dễ dàng viết pt BC
5 tháng 3 2021
Xét đường tròn (O) có: AM và AN là 2 tiếp tuyến cắt nhau tại A (gt)
\(\Rightarrow\) AM = AN (t/c 2 tiếp tuyến cắt nhau)
Mà AM = \(\dfrac{1}{2}\)AC; AN = \(\dfrac{1}{2}\)AB
\(\Rightarrow\) AB = AC
Xét tam giác ABC có: AB = AC (cmt)
\(\Rightarrow\) tam giác ABC cân tại A (đ/lí tam giác cân)
Chúc bn học tốt!
CH
Cô Hoàng Huyền
Admin
VIP
8 tháng 5 2017
a. Do ABC là tam giác cân tại A nên AB = AC hay AN = NB = CM = MA.
Xét tam giác AMB và ANC có:
AM = AN; AB = AC; góc A chung nên \(\Delta AMB=\Delta ANC\left(c-g-c\right)\)
b. Từ câu a, \(\widehat{ABM}=\widehat{ACN}\) (Hai góc tương ứng)
Mà tam giác ABC cân tại A nên \(\widehat{B}=\widehat{C}\)
Suy ra \(\widehat{DBC}=\widehat{DCB}\) hay tam giác BDC cân tại D.
c. Ta thấy \(\Delta ABE\) và \(\Delta ACE\) có : \(\widehat{B}=\widehat{C}=90^o;\) AB = AB; AE chung
nên \(\Delta ABE\)= \(\Delta ACE\left(ch-cgv\right)\Rightarrow EB=EC\)
Ta thấy AB = AC, DB = DC, EB = EC nên A, D, E cùng thuộc đường trung trực của BC. Vậy chúng thẳng hàng.
