Quả cầu khối lượng m=0,4kg gắn ở đầu một lò xo nằm ngang, đầu kia của lò xo cố định, độ cứng của lò xo k=40N/cm. Quả cầu có thế chuyển động không ma sát trên mặt phẳng ngang. Từ vị trí cân bằng, người ta kéo quả cầu cho lò xo dãn ra một đoạn 2cm rồi buông tay.
a) Tìm biểu thức xác đinh vận tốc của quả cầu khi nó ở cách vị trí cân bằng một đoạn x với |x|<xo.
b) Tính vận tốc cực đại của quả cầu trong quá trình chuyển đông. Vận tốc này đạt ở vị trí nào?

 10
10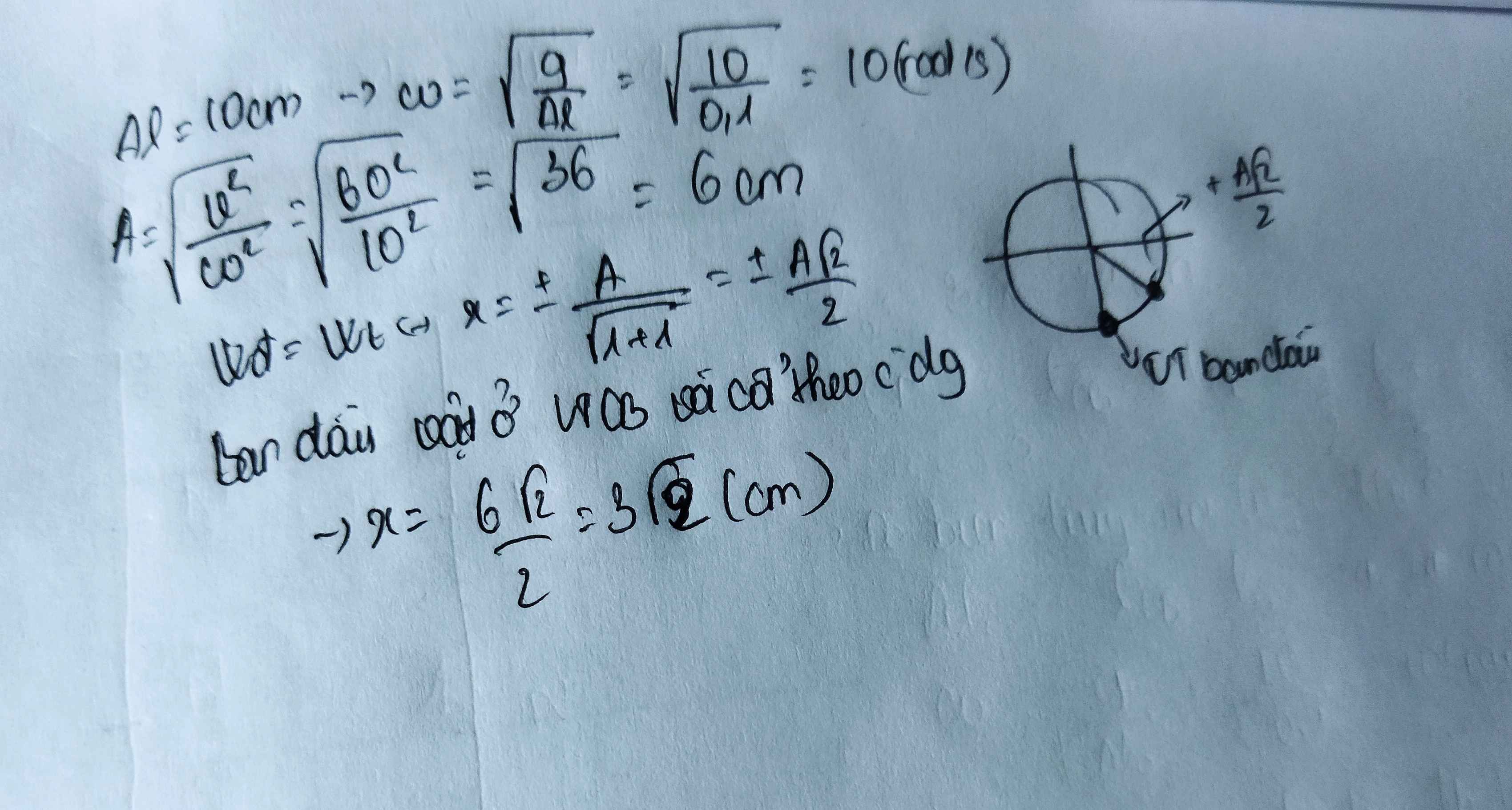




a/ \(W=\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2=\dfrac{1}{2}k\Delta l^2\)
\(\Leftrightarrow kx^2+mv^2=k\Delta l^2\Leftrightarrow v=\sqrt{\dfrac{k\Delta l^2-kx^2}{m}}=\sqrt{\dfrac{40.0,02^2-40x^2}{0,4}}\left(m/s\right)\)
b/ \(v_{max}\Leftrightarrow\dfrac{40.0,02^2-40x^2}{0,4}\left(max\right)\Leftrightarrow x=0\) => khi nó ở VTCB
\(\Rightarrow v_{max}=\dfrac{40.0,02^2}{0,4}\left(m/s\right)\)