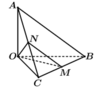
Cho tứ diện OABC có OA vuông góc (OBC) và OA=OB=OC, \(\widehat{BOC}=60^o\). Gọi M là trung điểm của AB. Tính cosin giữa hai đường thẳng OM và AB?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2021
Đề bài có vấn đề gì không nhỉ?
Tam giác OAB vuông cân tại O nên OM là trung tuyến đồng thời là đường cao
\(\Rightarrow OM\perp AB\) hay góc giữa OM và AB bằng 90 độ (cosin góc giữa 2 đường thẳng bằng 0)
18 tháng 3 2021
Bạn tự vẽ hình nhé!
Giả sử: OC = a ⇒ OB = 3/2a và OA = 3a
Xét tam giác OAB vuông tại O có: \(AB=\sqrt{OA^2+OB^2}=\dfrac{3\sqrt{5}}{2}a\)
\(\Rightarrow AM=BM=OM=\dfrac{1}{2}AB=\dfrac{3\sqrt{5}}{4}a\)
Xét tam giác OMA, có:
\(\cos\widehat{AOM}=\dfrac{OM^2+OA^2-AM^2}{2OM.OA}=\dfrac{OA}{2OM}=\dfrac{2\sqrt{5}}{5}\)
Xét tam giác OMB, có:
\(\cos\widehat{BOM}=\dfrac{OM^2+OB^2-BM^2}{2OM.OB}=\dfrac{OB}{2OM}=\dfrac{\sqrt{5}}{4}\)
Ta có: \(\overrightarrow{OM}.\overrightarrow{AB}=\overrightarrow{OM}\left(\overrightarrow{OB}-\overrightarrow{OA}\right)=\overrightarrow{OM}.\overrightarrow{OB}-\overrightarrow{OM}.\overrightarrow{OA}\)
\(=\dfrac{3\sqrt{5}}{4}a.\dfrac{3}{2}a.\dfrac{2\sqrt{5}}{5}-\dfrac{3\sqrt{5}}{4}a.3a.\dfrac{\sqrt{5}}{4}=\dfrac{-9}{16}a^2\)
\(\Rightarrow\cos\widehat{\left(\overrightarrow{OM},\overrightarrow{AB}\right)=\dfrac{\overrightarrow{OM}.\overrightarrow{AB}}{OM.AB}=-\dfrac{1}{10}}\)
\(\Rightarrow cos\left(OM,AB\right)=\dfrac{1}{10}\)
19 tháng 3 2021
Hicc, ở phần tính cos BOM mình bấm máy nhầm, bạn tự bấm lại nhé. :((((
Còn cả đoạn thay cos AOM và cos BOM vào tích vô hướng cũng bị lộn giữa 2 góc á.
Kết quả ra là 3/5 nhé!
Tự dưng giờ xem lại mới nhận ra lỗi sai nghiêm trọng này. Xin lỗi bạn nhé!
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2021
\(AB=\sqrt{OA^2+OB^2}=OA\sqrt{1+k^2}\)
\(OM=BM=\dfrac{1}{2}AB=\dfrac{OA}{2}\sqrt{1+k^2}\)
\(cos\widehat{OMB}=cos60^0=\dfrac{OM^2+BM^2-OB^2}{2OM.BM}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{OA^2\left(\dfrac{k^2+1}{4}\right)+OA^2\left(\dfrac{k^2+1}{4}\right)-k^2OA^2}{2.OA^2\left(\dfrac{k^2+1}{4}\right)}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{1-k^2}{1+k^2}=\dfrac{1}{2}\Rightarrow k^2=\dfrac{1}{3}\Rightarrow k=\dfrac{1}{\sqrt{3}}\)
CM
30 tháng 5 2017
Đặt
O
A
=
O
B
=
O
C
= a suy ra 
Gọi N là trung điểm AC, ta có MN//AB. Khi đó 
Trong tam giác OMN có 
nên OMN là tam giác đều
Chọn C.
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2021
Gọi N là trung điểm AC \(\Rightarrow MN||AB\Rightarrow\widehat{OMN}\) là góc giữa OM và AB
Đặt \(OA=a\)
\(AB=\sqrt{OA^2+OB^2}=\sqrt{a^2+k^2a^2}=a\sqrt{k^2+1}\)
\(AC=\sqrt{OA^2+OC^2}=a\sqrt{k^2+1}\)
\(BC=\sqrt{OB^2+OC^2}=a.k\sqrt{2}\)
\(MN=\dfrac{1}{2}AB=\dfrac{a}{2}\sqrt{k^2+1}\) ; \(OM=\dfrac{BC}{2}=a.\dfrac{k\sqrt{2}}{2}\) ; \(ON=\dfrac{1}{2}AC=a.\dfrac{\sqrt{k^2+1}}{2}\)
\(cos\widehat{OMN}=cos60^0=\dfrac{OM^2+MN^2-ON^2}{2OM.MN}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{a^2.\dfrac{k^2}{2}}{2.a^2.\dfrac{k\sqrt{2k^2+2}}{4}}=\dfrac{1}{2}\Leftrightarrow2k=\sqrt{2k^2+2}\)
\(\Leftrightarrow4k^2=2k^2+2\Rightarrow k=1\)
Tam giác OAB vuông cân tại O
\(\Rightarrow OM\perp AB\)
\(\Rightarrow\) cosin góc giữa 2 đường thẳng này bằng 0