Cho tam giác ABC nhọn hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh tam giác ABD đồng dạng tam giác ACE
b) Chứng minh BH.HD = CH.HE
c) Chứng minh Chứng tam giác ADE đồng dạng tam giác ABC
d) Gọi F là giao điểm của AH và BC, K là trung điểm của AH. Chứng minh: BF.CF = KF2 – HD2


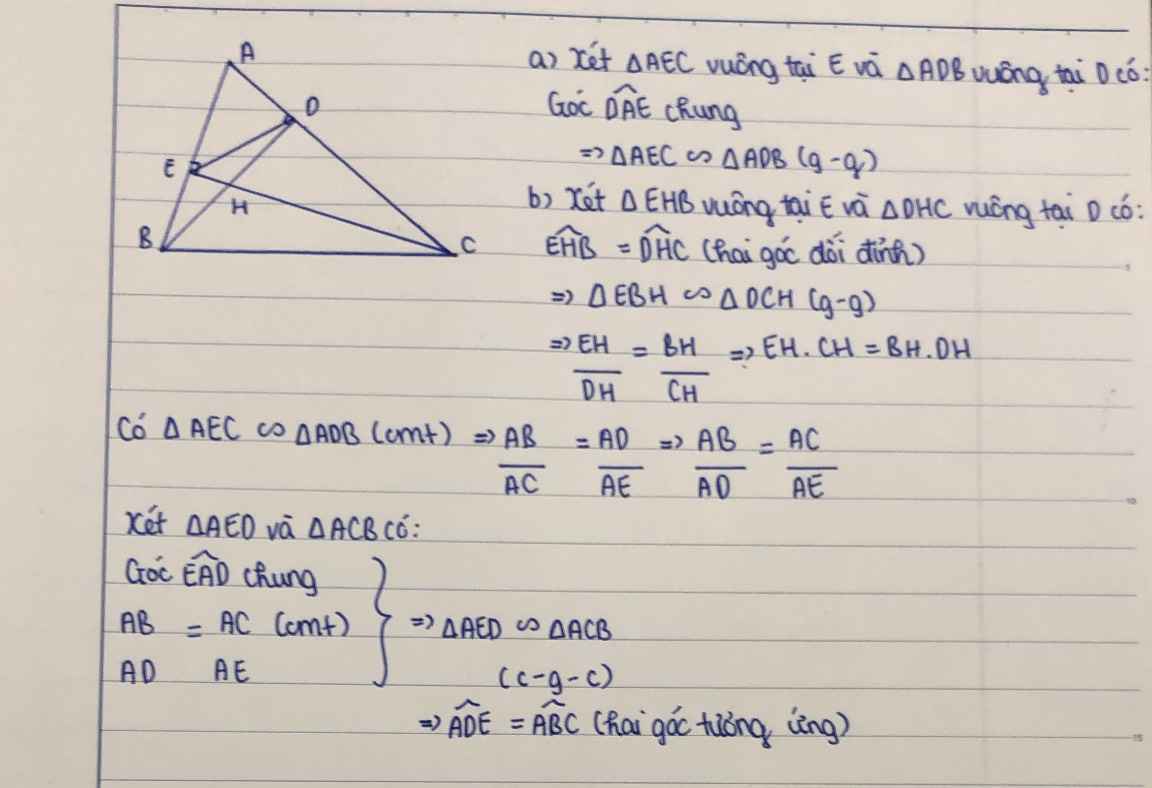
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔABD∼ΔACE(g-g)
b) Xét ΔEHB vuông tại E và ΔDHC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)(hai góc đối đỉnh)
Do đó: ΔEHB∼ΔDHC(g-g)
Suy ra: \(\dfrac{HE}{HD}=\dfrac{HB}{HC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(BH\cdot HD=CH\cdot HE\)(đpcm)