Một cây tre cao 8m bị gãy giữa thân, ngọn cây chạm đất cách gốc 4m. Hỏi điểm gãy cách gốc bao nhiêu m?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
21 tháng 3 2018
Gọi khoảng cách từ điểm gãy đến đất là x (m)
Giờ cây tre và mặt đất sẽ tạo thành tam giác vuông có 1 cạnh góc vuông là x (m), cạnh huyền là (8-x) và cạnh góc vuông còn lại là 4m
Theo Pitago ta có: (8-x)2=x2+16
<=> 64-8x+x2=x2+16 <=> 8x=64-16 <=> 8x=48
=> x=6 (m)
Đáp số: Điểm gãy cách đất 6 (m)
CM
16 tháng 2 2018
Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x CB = CD = 8 – x.
Vì ∆ ACD vuông tại A
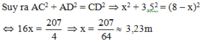
Vậy điểm gãy cách gốc cây 3,23m
Đáp án cần chọn là: B
18 tháng 2 2021
gọi k/c từ điểm gãy đến ngọn cây là x . Vì cây cau vuông góc với mặt đất nên cây cau gãy tạo với mặt đất hình tam giác vuông =>khoảng cách từ gốc đến điểm gãy và k/c từ ngọn cây đến góc là cạnh góc vuông và x là cạnh huyền Định Lí PTG ta có : 3^2+4^2=x^2 =>x=5 => chiều cao cây = 5+4=9m
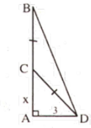
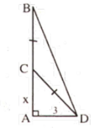
Điểm gãy cách gốc:
\(\sqrt{8^2-4^2}=4\sqrt{3}\left(m\right)\)
Tham khảo:
Gọi chiều dài phần còn lại là x (m)
Chiều dài phần gãy là 8−x (m)
Áp dụng định lí Pi-ta-go, ta có:
x2+42=(8−x)2
⇒x2+16=64−16x+x2
⇒x2−x2+16x=64−16
⇒16x=48
⇒x=3
Vậy điểm gãy cách gốc 3m