Question

[Phạm Kim Oanh]

Cho \(a;b;c\) là các số thực dương thỏa mãn :\(0< a;b;c< 1\). Chứng minh rằng:

\(\dfrac{1}{a.\left(1-b\right)}+\dfrac{1}{b.\left(1-c\right)}+\dfrac{1}{c.\left(1-a\right)}\ge\dfrac{3}{1-\left(a+b+c\right)+ab+bc+ac}\)

P/s:  Đề cương toán lớp 10 trường THPT chuyên sư phạm Hà Nội.
Em xin nhờ quý thầy cô giáo và các bạn giúp đỡ, em cám ơn nhiều ạ!

Answer 1

[Nguyễn Việt Lâm]

Đặt \(a\left(1-b\right)=x;b\left(1-c\right)=y;c\left(1-a\right)=x\)

\(\Rightarrow1-\left(a+b+c\right)+ab+bc+ca=1-a\left(1-b\right)-b\left(1-c\right)-c\left(1-a\right)=1-x-y-z\)

BĐT cần c/m trở thành:

\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\ge\dfrac{3}{1-x-y-z}\)

\(\Leftrightarrow\left(1-x-y-z\right)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)-3\ge0\)

\(\Leftrightarrow\dfrac{1-x-y-z}{x}+\dfrac{1-x-y-z}{y}+\dfrac{1-x-y-z}{z}-3\ge0\)

\(\Leftrightarrow\dfrac{1-y-z}{x}+\dfrac{1-z-x}{y}+\dfrac{1-x-y}{z}-6\ge0\) (1)

Lại có: \(1-y-z=1-b\left(1-c\right)-c\left(1-a\right)=1-b-c+bc+ca=\left(1-b\right)\left(1-c\right)+ca\)

Nên (1) tương đương:

\(\dfrac{\left(1-b\right)\left(1-c\right)+ca}{a\left(1-b\right)}+\dfrac{\left(1-a\right)\left(1-c\right)+ab}{b\left(1-c\right)}+\dfrac{\left(1-a\right)\left(1-b\right)+bc}{c\left(1-a\right)}-6\ge0\)

\(\Leftrightarrow\dfrac{1-c}{a}+\dfrac{c}{1-b}+\dfrac{1-a}{b}+\dfrac{a}{1-c}+\dfrac{1-b}{c}+\dfrac{b}{1-a}\ge6\)

BĐT trên hiển nhiên đúng theo AM-GM do:

\(\dfrac{1-c}{a}+\dfrac{c}{1-b}+\dfrac{1-a}{b}+\dfrac{a}{1-c}+\dfrac{1-b}{c}+\dfrac{b}{1-a}\ge6\sqrt[6]{\dfrac{abc\left(1-a\right)\left(1-b\right)\left(1-c\right)}{abc\left(1-a\right)\left(1-b\right)\left(1-c\right)}}=6\) (đpcm)

Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{2}\)

Answer 2

[Phạm Kim Oanh]

Cám ơn bài giải của thầy Lâm ạ!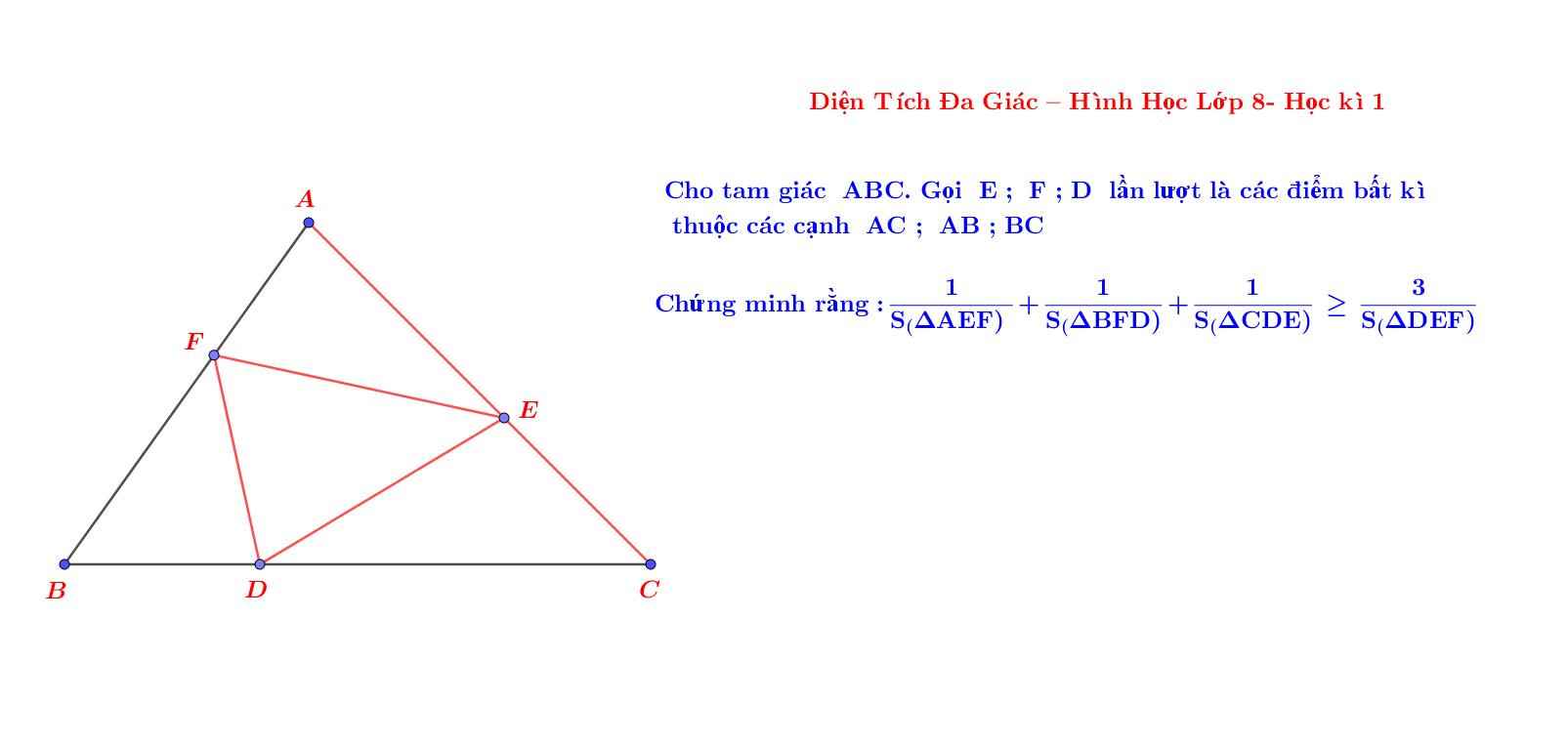
 Và từ bài bất đăng thức này, đã được chế thành bài toán hình học  trong 1 kì thi học sinh giỏi toán cấp tỉnh thầy ạ!