Mọi ngừi ơi giúp mk ý cuối cùng nhaCho \(\Delta\)\(ABC\) cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Kẻ BH vuông góc với AD tại H, kẻ CK vuông góc với AE tại K. Gọi I là giao điểm của hai đường thẳng BH và CK.CMR: AI là tia phân giác...
Đọc tiếp
Mọi ngừi ơi giúp mk ý cuối cùng nha
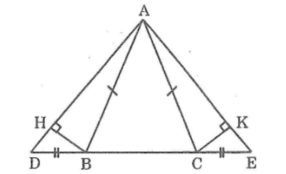
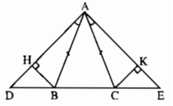
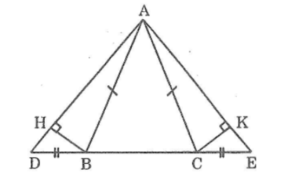
Cho \(\Delta\)\(ABC\) cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Kẻ BH vuông góc với AD tại H, kẻ CK vuông góc với AE tại K. Gọi I là giao điểm của hai đường thẳng BH và CK.
CMR: AI là tia phân giác của \(\widehat{DAE}\)
Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó:ΔABD=ΔACE
Suy ra: AD=AE
Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{HDB}=\widehat{KEC}\)
Do đó: ΔHBD=ΔKCE
Suy ra: \(\widehat{HBD}=\widehat{KCE}\)
mà \(\widehat{HBD}=\widehat{IBC}\)
và \(\widehat{KCE}=\widehat{ICB}\)
nên \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I
Xét ΔIBD và ΔICE có
IB=IC
\(\widehat{IBD}=\widehat{ICE}\)
BD=CE
Do đó: ΔIBD=ΔICE
Suy ra: ID=IE
Xét ΔADI và ΔAEI có
AD=AE
DI=EI
AI chung
Do đó: ΔADI=ΔAEI
Suy ra: \(\widehat{DAI}=\widehat{EAI}\)
hay AI là tia phân giác của góc DAE