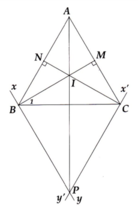
Cho tam giác ABC cân tại A. Một đường thẳng xy song song với đáy BC cắt cạnh AB tại D, cắt cạnh AC tại E. Vẽ BM vuông góc xy, CN vuông góc xy (M, N thuộc xy)
a) Chứng minh tam giác ADE cân
b) Chứng minh tam giác MBD = tam giác NCE
c) Vẽ DC cắt BE tại I. Chứng minh tam giác DBC = tam giác ECB rồi chứng minh tam giác IBC cân
d) Chứng minh AI là phân giác của góc BAC


a: Xét ΔABC có DE//BC
nên AD/AB=AE/AC
mà AB=AC
nên AD=AE
hay ΔADE cân tại A
b: Xét ΔMBD vuông tại M và ΔNCE vuông tại N có
BD=CE
\(\widehat{BDM}=\widehat{CEN}\)
Do đó: ΔMBD=ΔNCE
c: Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{ICB}=\widehat{IBC}\)
hay ΔIBC cân tại I
d: Ta có: IB=IC
nên I nằm trên đường trung trực của BC(1)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AI là đường trung trực của BC
Ta có: ΔABC cân tại A
mà AI là đường trung trực
nên AI là tia phân giác của góc BAC
bạn vẽ hình giúp mình đcko