cho 2,5 gam nhôm vào bình chứa 0,5 mol dung dịch axit sunfuric loãng
a,Viết phương trình phản ứng
b,chất nào còn dư sau phản ứng Tính khối lượng chất dư
c,Tính thể tích khí thoát ra ở điều kiện tiêu chuẩn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 2 2022
a: \(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\)
b: \(n_{Al}=\dfrac{2.5}{27}< \dfrac{1}{4}\)
=>H2SO4 dư, Al đủ
\(m_{H_2SO_4}=0.25\cdot98=24.5\left(g\right)\)
c: \(n_{Al_2\left(SO_4\right)_3}=\dfrac{2.5}{54}=\dfrac{5}{108}\left(mol\right)\)
\(\Leftrightarrow n_{H_2}=\dfrac{5}{36}\left(mol\right)\)
\(V_{H_2}=\dfrac{5}{36}\cdot22.4=\dfrac{28}{9}\left(lít\right)\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
10 tháng 2 2022
Mình thấy bạn Thịnh tính lượng dư sai
Đây là bài mình từng làm, bạn tham khảo nhé!
27 tháng 12 2020
PTHH: \(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\uparrow\)
Làm gộp các phần còn lại
Ta có: \(n_{Al}=\dfrac{5,4}{27}=0,2\left(mol\right)\) \(\Rightarrow\left\{{}\begin{matrix}n_{Al_2\left(SO_4\right)_3}=0,1mol\\n_{H_2SO_4}=n_{H_2}=0,3mol\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}V_{H_2}=0,3\cdot22,4=6,72\left(l\right)\\m_{Al_2\left(SO_4\right)_3}=0,1\cdot342=34,2\left(g\right)\\m_{H_2SO_4}=0,3\cdot98=29,4\left(g\right)\end{matrix}\right.\)
H
9 tháng 9 2021
a) $2Al + 3H_2SO_4 \to Al_2(SO_4)_3 + 3H_2$
b) $n_{Al} = 0,45(mol) ; n_{H_2SO_4} =\dfrac{219}{980} (mol)$
Ta thấy :
$n_{Al} : 2 > n_{H_2SO_4} : 3$ nên Al dư
Theo PTHH :
$n_{Al\ pư} = \dfrac{2}{3}n_{H_2SO_4} = \dfrac{73}{490} (mol)$
$m_{Al\ dư} = 12,15 - \dfrac{73}{490}.27 = 8,127(gam)$
c) $n_{Al_2(SO_4)_3} = \dfrac{1}{3}n_{H_2SO_4} = \dfrac{73}{930}(mol)$
$m_{muối} = \dfrac{73}{930}.342 = 25,48(gam)$
d) $V_{H_2} = \dfrac{219}{980}.22,4 = 5(lít)$
9 tháng 9 2021
Hình như đề sai
a,\(n_{Al}=\dfrac{12,15}{27}=0,45\left(mol\right)\)
\(m_{H_2SO_4}=109,5.20\%=21,9\left(g\right)\Rightarrow n_{H_2SO_4}=\dfrac{21,9}{98}=0,2235\left(mol\right)\)
9 tháng 9 2021
\(a/ Mg+H_2SO_4 \to MgSO_4+H_2\\ b/ n_{Mg}=\frac{3,6}{24}=0,15(mol)\\ n_{H_2SO_4}=0,168(mol)\\ b/\\ Mg \text{ hết}; H_2SO_4 \text{ dư}\\ n_{H_2SO_4(dư)}=0,168-0,15=0,018(mol)\\ m_{H_2SO_4}=0,018.98=1,764(g)\\ c/\\ n_{MgSO_4}=0,15(mol)\\ m_{MgSO_4}=0,15.120=18(g)\\ d/\\ n_{H_2}=0,15\\ V=0,15.22,4=3,36(l)\)
7 tháng 5 2022
a.b.\(n_{Al}=\dfrac{5,4}{27}=0,2mol\)
\(n_{H_2SO_4}=\dfrac{39,2}{98}=0,4mol\)
\(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\)
Xét: \(\dfrac{0,2}{2}\) < \(\dfrac{0,4}{3}\) ( mol )
0,2 0,3 0,1 0,3 ( mol )
\(m_{H_2SO_4\left(dư\right)}=\left(0,4-0,3\right).98=9,8g\)
\(m_{Al_2\left(SO_4\right)_3}=0,1.342=34,2g\)
c.\(2H_2+O_2\rightarrow\left(t^o\right)2H_2O\)
0,3 0,15 ( mol )
\(V_{kk}=V_{O_2}.5=\left(0,15.22,4\right).5=16,8l\)
22 tháng 3 2023
a, PT: \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
Ta có: \(n_{Al}=\dfrac{2,7}{27}=0,1\left(mol\right)\)
Xét tỉ lệ: \(\dfrac{0,1}{2}>\dfrac{0,25}{6}\), ta được Al dư.
Theo PT: \(n_{H_2}=\dfrac{1}{2}n_{HCl}=0,125\left(mol\right)\Rightarrow V_{H_2}=0,125.22,4=2,8\left(l\right)\)
b, Theo PT: \(n_{Al\left(pư\right)}=\dfrac{1}{3}n_{HCl}=\dfrac{1}{12}\left(mol\right)\Rightarrow n_{Al\left(dư\right)}=0,1-\dfrac{1}{12}=\dfrac{1}{60}\left(mol\right)\)
\(\Rightarrow m_{Al}=\dfrac{1}{60}.27=0,45\left(g\right)\)
16 tháng 2 2022
\(n_{Fe}=\dfrac{11,2}{56}=0,2\left(mol\right)\)
PTHH : Fe + 2HCl -> FeCl2 + H2
0,2 0,4 0,2
Xét tỉ lệ \(\dfrac{0,2}{1}< \dfrac{0,5}{2}\) => Fe đủ , HCl dư
\(m_{HCl\left(dư\right)}=\left(0,5-0,4\right).36,5=3,65\left(g\right)\)
\(V_{H_2}=0,2.22,4=4,48\left(l\right)\)
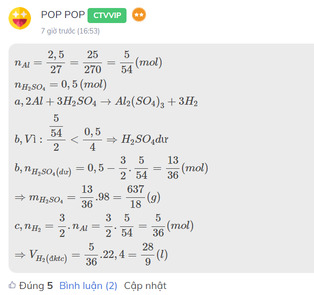
\(n_{Al}=\dfrac{2,5}{27}=\dfrac{25}{270}=\dfrac{5}{54}\left(mol\right)\\ n_{H_2SO_4}=0,5\left(mol\right)\\ a,2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\\ b,Vì:\dfrac{\dfrac{5}{54}}{2}< \dfrac{0,5}{4}\Rightarrow H_2SO_4dư\\ b,n_{H_2SO_4\left(dư\right)}=0,5-\dfrac{3}{2}.\dfrac{5}{54}=\dfrac{13}{36}\left(mol\right)\\ \Rightarrow m_{H_2SO_4}=\dfrac{13}{36}.98=\dfrac{637}{18}\left(g\right)\\ c,n_{H_2}=\dfrac{3}{2}.n_{Al}=\dfrac{3}{2}.\dfrac{5}{54}=\dfrac{5}{36}\left(mol\right)\\ \Rightarrow V_{H_2\left(đktc\right)}=\dfrac{5}{36}.22,4=\dfrac{28}{9}\left(l\right)\)