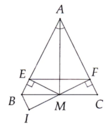
Đề bài: Cho ΔABC cân tại A. Tia phân giác góc BAC cắt cạnh BC tại M.a) Chứng minh: ΔAMB = ΔAMC b) Kẻ ME ⊥ AB (E∈AB), MF ⊥ AC (F∈AC). Chứng minh ΔAEF cânc) Chứng minh: AM ⊥ EF d) Qua B kẻ đường thẳng song song với AC cắt đường thẳng FM tại I. Chứng minh: BE=BI (Các bạn chứng minh chi tiết giúp mik vs...
Đọc tiếp
Đề bài: Cho ΔABC cân tại A. Tia phân giác góc BAC cắt cạnh BC tại M.
a) Chứng minh: ΔAMB = ΔAMC
b) Kẻ ME ⊥ AB (E∈AB), MF ⊥ AC (F∈AC). Chứng minh ΔAEF cân
c) Chứng minh: AM ⊥ EF
d) Qua B kẻ đường thẳng song song với AC cắt đường thẳng FM tại I. Chứng minh: BE=BI
(Các bạn chứng minh chi tiết giúp mik vs ạ)
AB) và MF vuông góc với AC (F 
a, Vì góc BM là tia phân giác góc BAC nên=> góc BAM= góc MAC
Vì tam giác ABC cân tại A=>AB=AC(t/c)
Xét tam giác AMB và tam giác AMC, ta có:
AB=AC(cmt)
AM(cạnh chung)
góc BAM=góc MAC(cmt)
=>Tam giác AMB=tam giác AMC(c.g.c)
a: Xét ΔAMB và ΔAMC có
AM chung
\(\widehat{BAM}=\widehat{CAM}\)
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF
hay ΔAEF cân tại A
c: Ta có: ΔAEF cân tại A
mà AM là đường phân giác
nên AM là đường cao